차원(Dimension)
공간 내 데이터의 위치를 나타내기 위해 필요한 축의 개수

- 좌표상 표현할 수 있는 표현은 3차원까지입니다.
- 그 이상 넘어가면 변수가 늘어나면서 차원이 커짐에 따라 공간을 설명하기 위한 데이터 부족
- 과적합 & 성능 감소 & 정보의 밀도 감소
차원 축소(Dimensionality Reduction)
데이터를 잘 설명할 수 있는 변수의 개수는 현재 변수의 개수보다 작을 수 있습니다. 데이터를 기반으로 잠재 공간을 파악하는 것이고 이로 인해 차원의 저주 해결, 연산량 감소, 시각화 용이 등의 이점이 있습니다.
변수 선택(Feature Selection)
원본 데이터의 변수 중 불필요한 변수를 제거하는 방법입니다.
ex) 몸무게, 키, 머리 길이 -> 몸무게, 키
변수 추출(Feature Extraction)
원본 데이터의 변수들을 조합해 새로운 변수를 생성하는 방법입니다.
키, 몸무게, 머리 길이 -> 체구, 머리 길이
체구 = 0.3 * 몸무게 + 0.7 * 키
PCA(Principal Component Analysis)
여러 변수의 정보를 담고 있는 주성분(Principal Component)이라는 새로운 변수를 생성하는 차원 축소 기법
단순히 차원을 줄이기보다는 관측된 차원이 아닌 실제 데이터를 설명하는 차원을 찾아서 데이터를 잘 이해하고자 함
분산이 최대로 하는 축에 정사영 시킵니다. 이렇게 해야 데이터의 손실이 가장 적습니다.


두 번째 주성분은 첫 번째 벡터에 직교하는 축에 정사영 시킵니다.
주성분 축을 찾는 방법
1. 데이터 표준화
데이터를 표준화하지 않으면 값의 크기에 따라 공분산이 영향을 받음

2. 공분산 행렬 생성
X = {(2, 1), (2, 4), (4, 1), (4, 3)}
E(X) = 1/4 * (2 +2 + 4 +4) = 3
Var(x) = 1/4 * ((-1)^2 +(-1)^2 +1^2 + 1^2) = 1
E(Y) = 1/4 * (1+4+1+3) = 2.25
Var(Y) = 1/4 * ((-1.25)^2 +1.75^2 + (-1.25)^2 +0.75^2) = 1.6875
Cov(X, Y) = E((X - E(X))(Y - E(Y)) = 1/4 *((-1 *-1.25) + (-1 *1.75) + (1 * -1.25) + (1 * 0.75)) = -0.25
Con(Y, X) = E((Y- E(Y))(X - E(X)) = -0.25

3. 교윳값 분해(Eigen Decomposition)


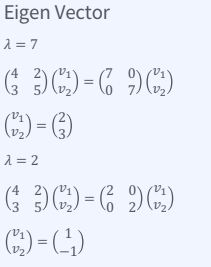
4. K개 벡터의 새로운 Basis
K를 선택하는 방법
- Scree Plot
- Explained
PCA의 장점
- 변수간 상관관계 및 연광성을 이용해 변수를 생성합니다.
- 차원 축소로 차원의 저주를 해결할 수 있습니다.
PCA의 단점
- 데이터에 선형성이 없다면 적용할 수 없습니다.
- 데이터의 클래스를 고려하지 않기 때문에 최대 분산 방향이 특징 구분을 좋게 한다고 보장할 수 없습니다.
- 도메인 지식이 필요합니다.
LDA(Linear Discriminant Analysis)
데이터의 분포를 학습하여 분리를 최적 하하는 결정 경계를 만들어 데이터를 분류하는 모델
PDA와 반대로 지도 학습에서 사용됩니다. 클래스 간의 분산을 크게, 클래스 내의 분산을 작게 하는 것입니다.

PCA
비지도 학습
데이터 전체의 분포를 참고 -> 새로운 basis 설정 -> 그 축에 맞게 데이터를 새롭게 Projection
LDA
지도 학습
지도적인 방법으로 Basis를 찾아 -> 그 축을 분리에 이용 -> 최적의 분리를 완성한 뒤 projection
t-Stochastic Neighbor Embedding (t-SNE)
고차원의 데이터를 저 차원의 데이터로 거리 관계를 유지하며 Projection 하는 기법
학습 방법
- 랜덤 순서로 나열
- 데이터 하나에 대해서 동일 군집은 당기는 힘 / 다른 군집은 미는 힘 계산
- 데이터를 힘의 균형에 맞는 위치로 이동
- 모든 점들에 대해서 2~3 과정 반복
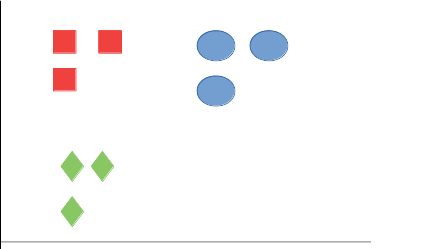
Step 1) 랜덤 순서로 나열

Step 2) 데이터 하나에 대해서 동일 군집은 당기는 힘 / 다른 군집은 미는 힘 계산
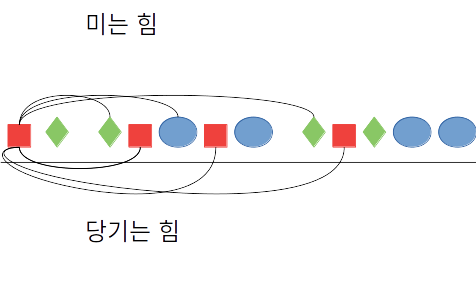
Step 3) 데이터를 힘의 균형에 맞는 위치로 이동

Step 4) 모든 점들에 대해서 2~3 과정 반복

t-SNE 장점
직관적으로 데이터의 구조를 시각화 아여 확인할 수 있다.
t-SNE 단점
- 거리를 학습하여 계속 업데이트하기 때문에 값이 매번 바뀜
- PCA와 LDA와 다르게 결과를 변수로 사용할 수 없음.
- 데이터 수가 많아지면 시간이 오래 걸림
'머신러닝' 카테고리의 다른 글
| [머신러닝] 추천 시스템 (0) | 2022.05.12 |
|---|---|
| [머신러닝] 이상 탐지(Anomaly Detection) (0) | 2022.05.11 |
| [머신러닝] 군집화 (0) | 2022.05.06 |
| [머신러닝] SVM (0) | 2022.05.06 |
| [머신러닝] K-Nearest Neighbors (0) | 2022.05.06 |




댓글