군집화(Clustering)의 정의

유사한 속성을 갖는 데이터들을 묶어 전체 데이터들 몇 개의 군집으로 나누는 것입니다.
Classification
- Supervised Learning
- 소속 집단의 정보를 알고 있는 상태
- Label이 있는 데이터를 나누는 방법
Clustering
- Unsupervised Learning
- 소속 집단의 정보를 모르고 있는 상태
- Label이 없는 데이터를 나누는 방법
계층적 군집화
- 개체들을 가까운 집단부터 묶어 나가는 방식
- 유사한 개체들이 결합되는 dendrogram 생성
- Cluster들은 sub-cluster를 갖고 있다.

개체들을 가까운 집단부터 묶어 나가는 방식입니다.
- 거리의 종류
- 유클리드 거리
- 맨해튼 거리
- 표준화 거리
- 민콥 스키 거리
- 최단 연결법
- 최장 연결법
- 평균 연결법
- 중심 연결법
최단 연결법
군집에서 가장 가까운 데이터가 새로운 거리가 됩니다.

최장 연결법
군집에서 가장 먼 데이터가 새로운 거리가 됩니다.

평균 연결법
군집의 데이터들 간의 거리의 평균이 군집과 데이터의 거리가 됩니다.

중심 연결법
군집의 중심이 새로운 거리가 됩니다.

최단 거리로 예시를 들어보겠습니다.

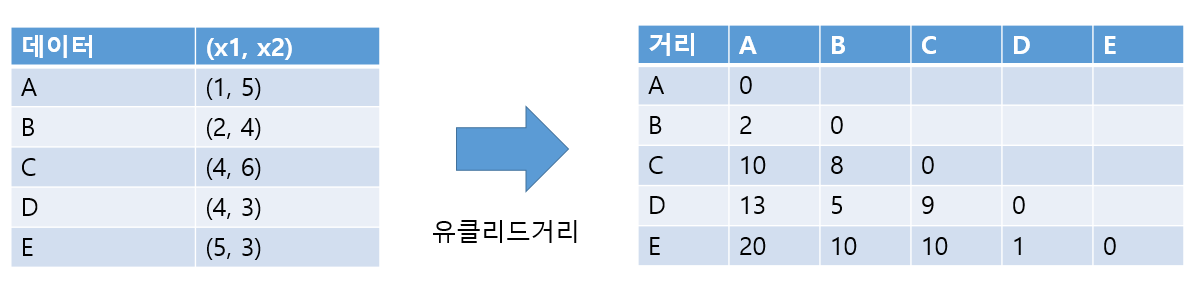
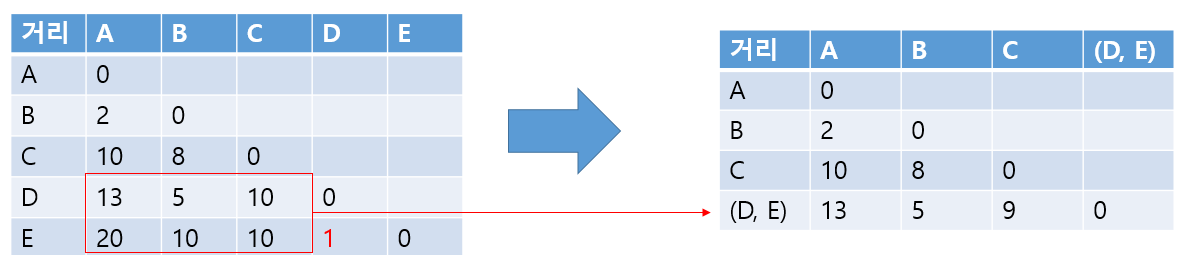
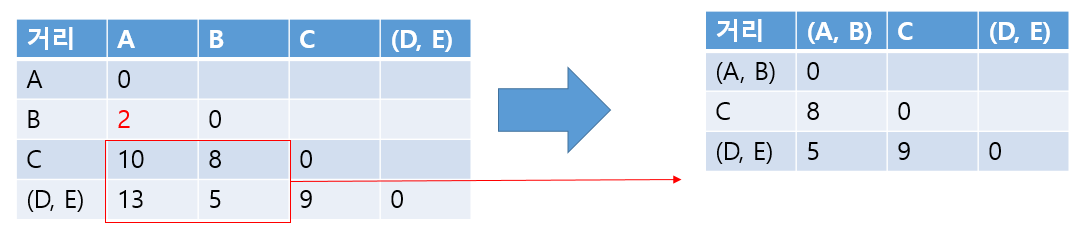
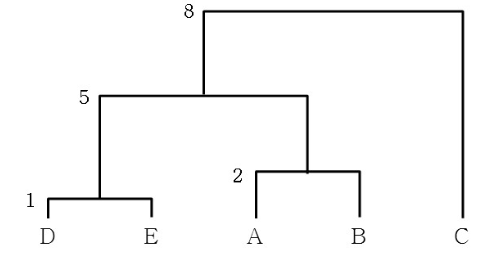

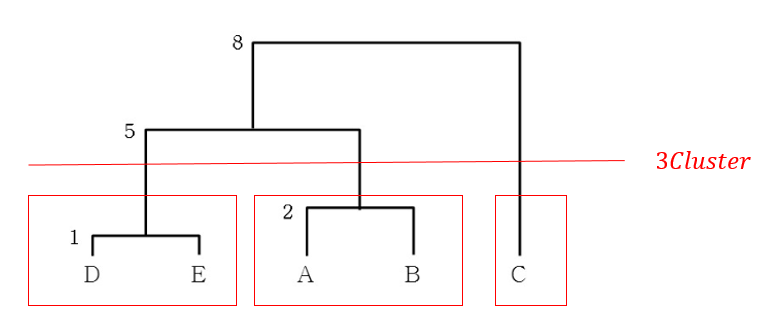
군집 내 유사도를 최대화(거리를 최소화), 군집 간 유사도를 최소화 (거리를 최대화) 될수록 좋은 모델입니다.
같은 군집끼리의 거리는 가깝고, 다른 군집 간의 거리는 멀수록 좋다는 의미입니다.
평가 방법
- Dunn Index
- DI = 군집과 군집 사이의 거리 중 최솟값 / 군집 내 데이터 간 거리 중 최댓값
- 군집과 군집 사이의 거리가 클수록, 군집 내 데이터 간 거리가 작을수록 좋은 모델
- Silhouette Index
- S = (b(i) - a(i)) / max {a(i), b(i)}
- a(i)[군집 내 응집도]: 데이터 xi와 동일한 군집 내의 나머지 데이터들과 평균 거리
- b(i)[군집 간 분리도]: 데이터 xi와 가장 가까운 군집 내의 모든 데이터들과 평균 거리
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram
def plot_dendrogram(model, **kwargs):
counts = np.zeros(model.children_.shape[0])
n_samples = len(model.labels_)
for i, merge in enumerate(model.children_):
current_count = 0
for child_idx in merge:
if child_idx < n_samples:
current_count += 1 # leaf node
else:
current_count += counts[child_idx - n_samples]
counts[i] = current_count
linkage_matrix = np.column_stack([model.children_, model.distances_,
counts]).astype(float)
dendrogram(linkage_matrix, **kwargs, labels=["A", "B", "C", "D", "E"])
data = np.array(
[
(1, 5),
(2, 4),
(4, 6),
(4, 3),
(5, 3),
]
)
single_cluster = AgglomerativeClustering(
n_clusters=2, linkage='single'
)
single_cluster.fit(data)
print(single_cluster.labels_)
plt.figure(figsize=(7, 7))
plt.scatter(data[:, 0], data[:, 1], c=single_cluster.labels_)
for i, txt in enumerate(["A", "B", "C", "D", "E"]):
plt.annotate(txt, (data[i, 0], data[i, 1]))array([0, 0, 1, 0, 0])
클러스터를 2개로 묶은 결과입니다.
single_cluster_3 = AgglomerativeClustering(
n_clusters=3, linkage='single'
)
single_cluster_3.fit(data)
print(single_cluster_3.labels_)
plt.figure(figsize=(7, 7))
plt.scatter(data[:, 0], data[:, 1], c=single_cluster_3.labels_)
for i, txt in enumerate(["A", "B", "C", "D", "E"]):
plt.annotate(txt, (data[i, 0], data[i, 1]))
single_cluster_3 = AgglomerativeClustering(
n_clusters=3, linkage='single'
)
single_cluster_3.fit(data)
print(single_cluster_3.labels_)
plt.figure(figsize=(7, 7))
plt.scatter(data[:, 0], data[:, 1], c=single_cluster_3.labels_)
for i, txt in enumerate(["A", "B", "C", "D", "E"]):
plt.annotate(txt, (data[i, 0], data[i, 1]))[0 0 1 2 2]
위는 3개로 묶은 결과입니다. 마지막으로 평균, 최장, 최소, 중심의 덴드로그램을 보겠습니다.
# average: 평균, complete: 최장, single: 최단, ward: 중심
avg_cluster = AgglomerativeClustering(distance_threshold=0, n_clusters=None, linkage='average')
max_cluster = AgglomerativeClustering(distance_threshold=0, n_clusters=None, linkage='complete')
single_cluster = AgglomerativeClustering(distance_threshold=0, n_clusters=None, linkage='single')
centroid_cluster = AgglomerativeClustering(distance_threshold=0, n_clusters=None, linkage='ward')
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(15, 10))
for idx, (name, cluster) in enumerate(clusters):
cluster.fit(data)
ax = axes[idx//2, idx%2]
ax.set_title(f'Hierarchical Clustering Dendrogram with {name} linkage')
plot_dendrogram(cluster, truncate_mode='level', p=3, ax=ax)
비계층적(Non-Hierarchical) 군집화
- 전체 데이터를 확인하고 특정한 기준으로 데이터를 동시에 구분합니다.
- 각 데이터들은 사전에 정의된 개수의 군집 중 하나에 속하게 됩니다.

K-Means
K-평균은 군집 중심점이라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 기법
- 데이터 중 임의의 K개의 중심점(Centroid) 설정합니다.
- 모든 데이터에서 설정된 각 군집의 중심점까지의 거리를 계산합니다.
- 모든 데이터를 가장 가까운 중심점에 속한 군집으로 할당합니다.
- 각 군집의 중심점을 재설정합니다.
- 군집의 중심점이 변경되지 않을 때까지 2~5를 반복합니다.
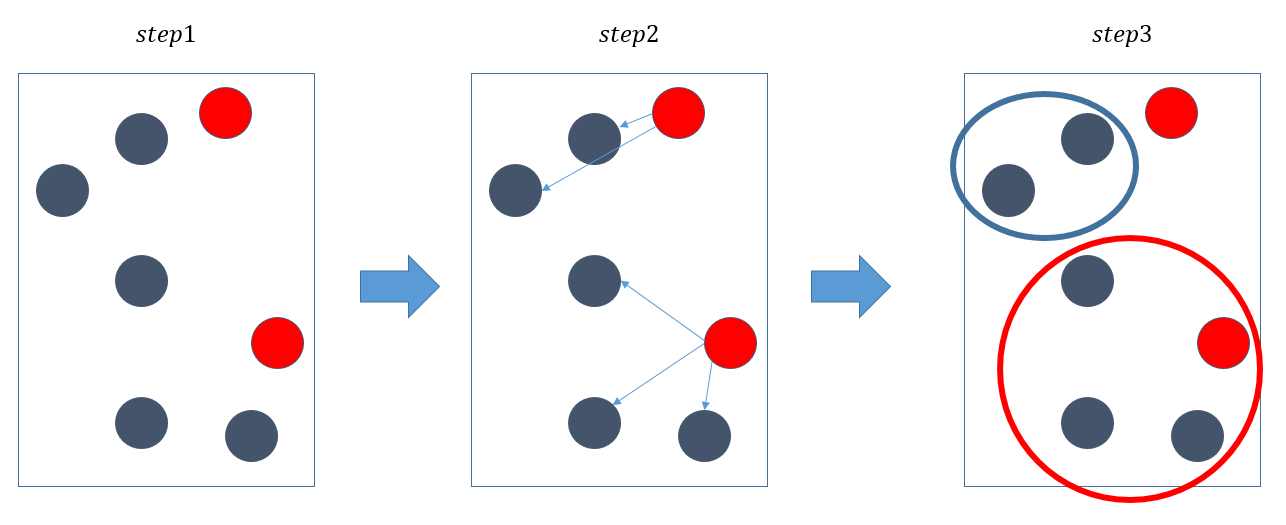
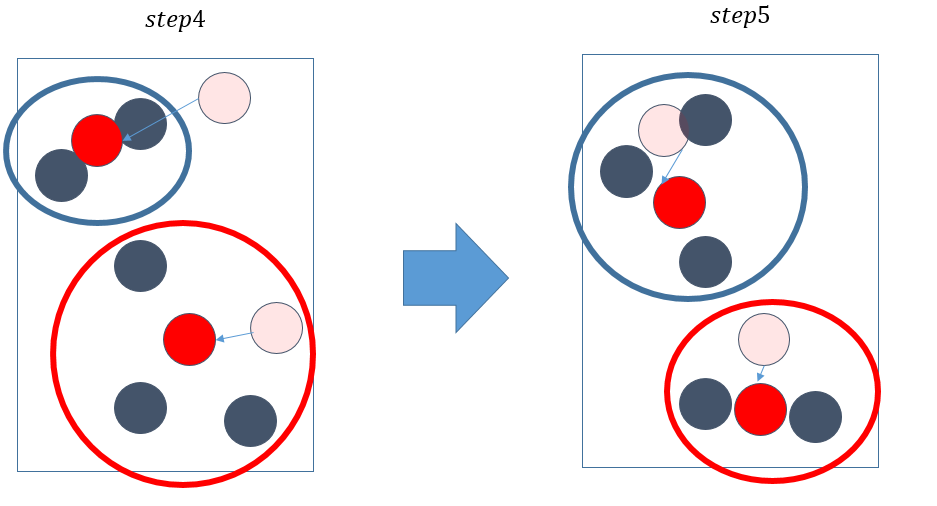
초기 중심점 설정
- K-평균의 성능은 초기 중심점의 위치에 크게 좌우됩니다.
- 무작위로 초기 중심 설정되는 위험을 방지하기 위한 다양한 방법이 있습니다.
- 반복적으로 수행하여 가장 많이 나타나는 군집을 사용
- 전체 데이터 중 일부만 추출하여 계층적 군집화를 수행한 뒤 초기의 군집 중심을 설정
- 데이터 분포의 정보를 사용하여 초기 중심 설정
SSE(Sum of Squared Error)
관측치와 중심들 사이의 거리


그래프가 꺾이는 지점을 ElbowPoint라 하는데 이 지점으로 군집을 정하면 됩니다.
장점
- Kmeans는 적용하기가 쉽습니다.
- 새로운 데이터에 대한 군집을 계산할 때 각 군집의 중심점과 거리만 계산하면 되기 때문에 빠릅니다.
단점
- 서로 다른 크기의 군집을 잘 못 찾습니다.
- 서로 다른 밀도의 군집을 잘 못 찾습니다.
- 지역적 패턴이 존재하는 군집을 잘 못 찾습니다.
- 반복 횟수가 많을 경우 수행 시간이 매우 느려집니다.
- 거리 기반 알고리즘으로 속성의 개수가 매우 많을 경우 정확도가 떨어집니다(이를 위해 PCA 차원 감소를 적용해야 할 수도 있음)

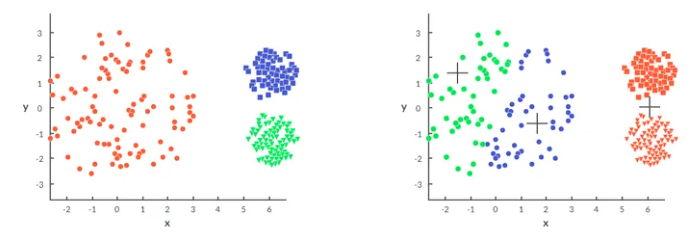
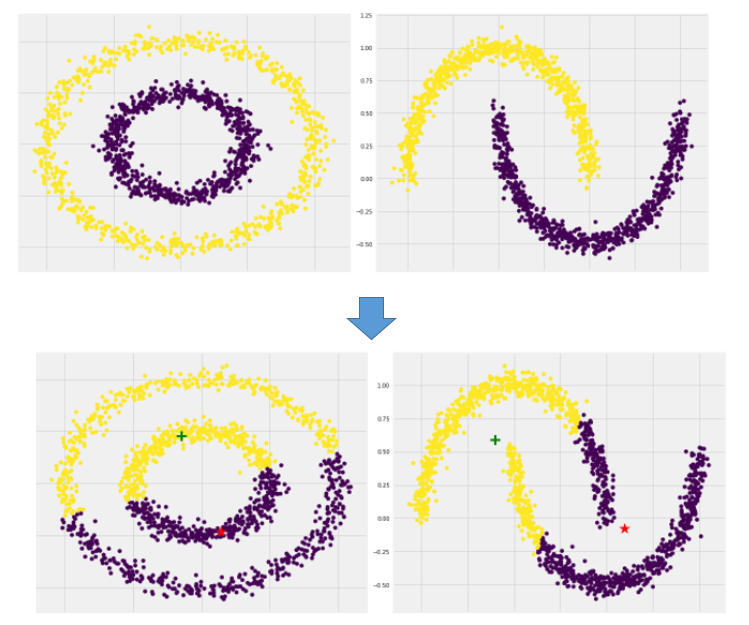
DB SCAN(Density-Based Spatial Clustering of Applications with Noise)
클러스터링 알고리즘 중 밀도 방식의 클러스터링을 사용합니다. 앞서 말한 K-Means는 군집 간의 거리를 이용하는 방법인데, 밀도 기반 클러스터링은 점이 세밀하게 몰려 있거나 밀도가 높은 부분을 클러스터링 하는 방식입니다.
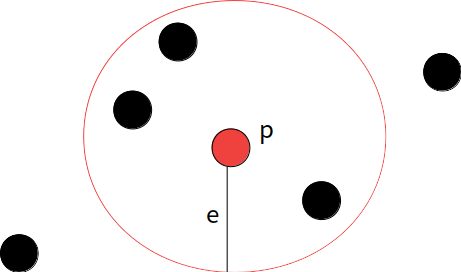
점 P에서부터 거리가 e(epslion) 내에 m(minPts) 개 이상 있으면 하나의 군집으로 인식
학습방법
- Core Points
- 거리 eps이내에 데이터가(자신 포함) minPts개 이상 있는 포인트
- Border Points
- Core Points를 이웃으로 갖고 있지만 eps 이내에 데이터가 minPts개 보다 적은 포인트
- Noise Point
- Core Points를 이웃으로 갖고 있지 않고 eps 이내에 데이터가 minPts개 보다 적은 포인트
Step 1) Core Points
minPts = 4 일 때 예시


Step 2) Boerder Points
Core Points를 이웃으로 갖고 있지만 eps 이내에 데이터가 minPts개 보다 적은 포인트
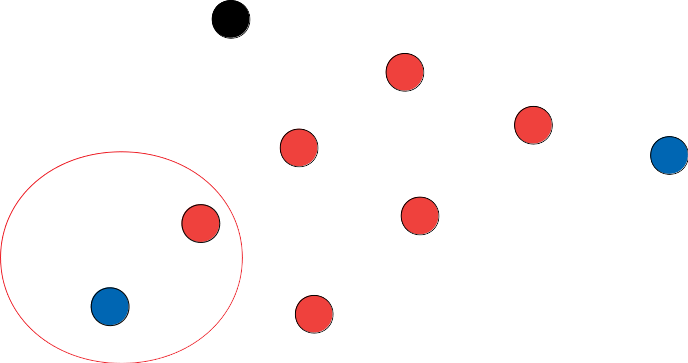
Step 3) Noise Points
Core Points를 이웃으로 갖고 있지 않고 eps 이내에 데이터가 minPts개 보다 적은 포인트
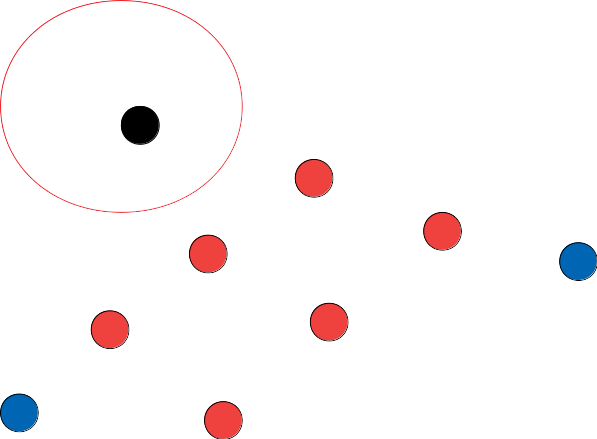
Result
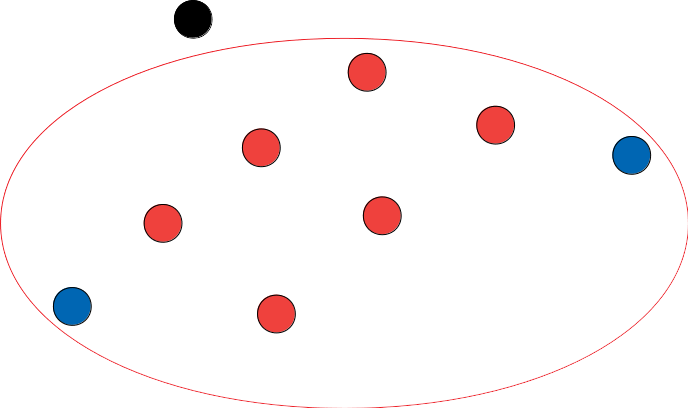
minPts
- 최적의 minPts를 구하는 방법에 대해서는 알려진 방법이 없다.
- Cross Validation 등의 방법으로 구해야 함
Eps
- 주어진 minPts에 대한 최적의 거리를 구하는 사업에 대해서는 K-dist Graph를 사용합니다.
K-Dist Graph
- minPts번째 인접한 이웃 데이터 포인트까지의 거리
- 급격히 증가하지 직전의 지점을 eps로 설정해야 함
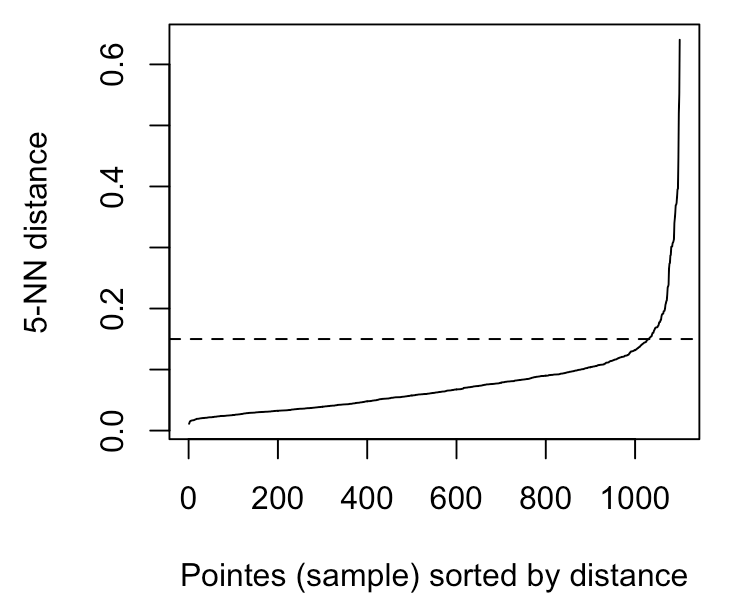
1000 부근 꺾이는 지점으로 설정합니다
- 지역적 패턴이 있는 데이터의 군집도 찾을 수 있습니다.
- 노이즈 데이터를 따로 분류하여 노이즈 데이터들이 군집에 영향을 주지 않는다
- 하지만 밀도 구역에 따라 바뀔 경우를 파악하지 못함

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
data, label = make_blobs(n_samples=1500, random_state=170)
correct_kmeans = KMeans(n_clusters=3)
correct_kmeans.fit(data)
correct_pred = correct_kmeans.predict(data)
correct_center = correct_kmeans.cluster_centers_
print("중심 좌표 : \n", correct_center)
print("예측 라벨 : ", correct_pred)
plt.scatter(data[:, 0], data[:, 1], c=correct_pred)
plt.scatter(correct_center[:, 0], correct_center[:, 1], marker='*', s=100, color='red')중심 좌표 :
[[-4.55490993 0.02920864]
[ 1.91176144 0.40634045]
[-8.94137566 -5.48137132]]
예측 라벨 : [0 0 2 ... 1 1 1]
sse_per_n = []
for n in range(1, 12, 2):
kmeans = KMeans(n_clusters=n)
kmeans.fit(data)
sse_per_n += [kmeans.inertia_] # 응집도
plt.plot(range(1, 12, 2), sse_per_n)
plt.title('Sum of Squared Error')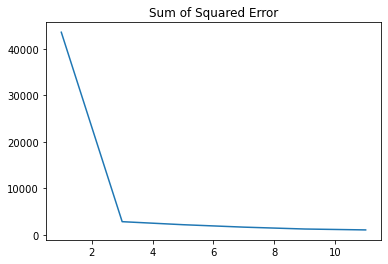
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
pattern_data = np.dot(data, transformation)
pattern_kmeans = KMeans(n_clusters=3, random_state=2021)
pattern_pred = pattern_kmeans.fit_predict(pattern_data)
pattern_center = pattern_kmeans.cluster_centers_
plt.scatter(pattern_data[:, 0], pattern_data[:, 1], c=pattern_pred)
plt.scatter(pattern_center[:, 0], pattern_center[:, 1], marker='*', s=100, color='red')
지역적 패턴이 있는 데이터는 KMeans로 분류하기 어렵습니다. DBSCAN을 사용합니다.
from sklearn.cluster import DBSCAN
pattern_db = DBSCAN(eps=.4, min_samples=20)
pattern_db_pred = pattern_db.fit_predict(pattern_data)
plt.scatter(pattern_data[:, 0], pattern_data[:, 1], c=pattern_db_pred)

'머신러닝' 카테고리의 다른 글
| [머신러닝] 이상 탐지(Anomaly Detection) (0) | 2022.05.11 |
|---|---|
| [머신러닝] 차원축소 (0) | 2022.05.10 |
| [머신러닝] SVM (0) | 2022.05.06 |
| [머신러닝] K-Nearest Neighbors (0) | 2022.05.06 |
| [머신러닝] Naive Bayes (0) | 2022.05.06 |




댓글