참조
[논문리뷰] DETR: End-to-End Object Detection with Transformer
들어가며 본 논문은 Object Detection과 Transformer의 사전 지식이 있다는 가정하에 작성되었습니다. 오늘 리뷰할 논문은 DETR입니다. 이 논문은 Object Detection에 Transformer를 적용시킨 최초의 논문입니다.
lcyking.tistory.com
들어가며
Anchor DETR은 DETR을 기반으로 작성된 논문입니다. 기존 DETR은 Transformer 구조를 Obect Detection에 처음으로 적용하면서 큰 관심을 이끌었습니다. 하지만 객체를 추정하는 Object Queries가 어떤 의미를 가지는지 명확하지 않고, 어느 영역에 초점을 두는지에 대한 모호성이 존재한다는 제한점이 있습니다.
본 논문에서는 이러한 제한점을 개선하고자, 일반적으로 CNN이 Object Detection을 수행할 때 사용하는 Anchor에 대한 개념을 도입하였습니다. CNN은 이 Anchor의 위치를 조정하면서 명확하게 객체를 가리키기 때문에, 위 제한점들을 해결할 수 있다고 주장하고, 아래 그림이 이 주장에 대한 근거입니다.

위 그림은 Object Queries가 어느 위치를 참조할지에 대한 그림인데, 확연하게 차이가 나는 것을 볼 수 있습니다. 이러한 근거로 각 쿼리가 객체를 잘 나타내며, 이는 최적화를 더 쉽게 할 수 있다는 장점이 있습니다.
또한, 한 앵커에 아래와 같이 여러 객체가 나타날 수 있는 경우를 생각하여, 앵커에 대응하는 쿼리에 Multi Pattern의 개념을 적용하였습니다.
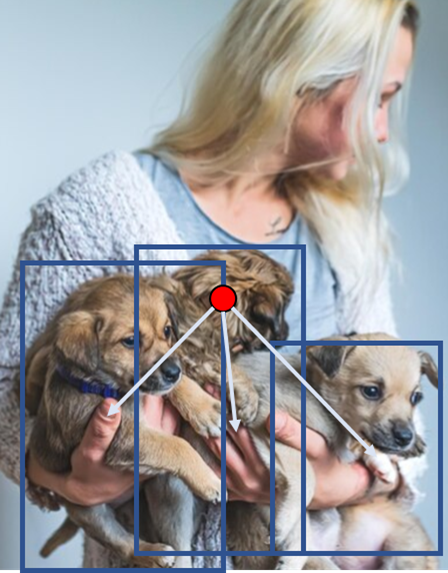
마지막으로, 기존 Attention의 연산은 메모리와 계산량이 해상도가 올라가면 기하급수적으로 올라가기 때문에, 전체 해상도에 대한 Attention이 아닌 Row, Column으로 각각 나누어 연산하는 Row-Column Decouple Attention(RCDA)를 제안하였습니다. 이에 대한 결과로 메모리의 효율성과 동시에 더 나은 성능을 기록했다고 합니다.
정리하자면 본 논문에서 제안하는 기술은 총 3가지입니다:
- 앵커의 개념을 도입
- 각 앵커와 대응되는 쿼리에 Multi Pattern의 개념을 적용
- 기존 Attention을 RCDA로 변경
이제 이 3가지 기술을 어떻게 적용하는지 살펴보겠습니다.
Anchor DETR
먼저 기존 CNN에서 사용된 앵커들은 2D 좌표(x, y)를 사용하였고, 균등한 그리드 좌표였습니다. 본 논문은 이 타입 및 나아가 학습된 앵커도 사용하여 비교 실험을 진행하였습니다.

솔직히 결과는 0.1 정도로 차이가 크게 없습니다.
Anchor Points to Object Query
위 앵커는 그냥 2D 좌표를 사용한다 정도로 아시면 될 것이고, 주목할 점은 이 앵커를 어떻게 Object Queries에 위치 정보로 주입하냐는 것입니다. 기존에는 Object Queries \(Q_f \in \mathbb {R}^{N_q * C} \)를 임베딩의 형태로 생성하고, sine-cosine position embedding이나 learned embedding으로 쿼리와 동일한 차원으로 위치 정보를 삽입하였습니다.
그렇다면, 앵커에 대한 위치 정보 \(Pos_q \in \mathbb {R}^{N_A * 2} \)도 Object Queries와 동일한 차원 (\(N_q, C \)) 의 형태로 만들어 주어야 합니다. 본 논문에서는 앵커의 2D 좌표(x, y)를 sine-consine position encoding 함수로 C차원의 형태로 만들고, MLP network에 입력하였습니다. MLP network는 입력과 출력이 동일한 2개의 Linear layers를 구성하였습니다.

위 g는 sine-consine + MLP로 구성된 Position Encoding 함수입니다.
Multiple Prediction for Each Anchor Point
다음은 제안된 기술의 2번째인 한 앵커에 대응되는 쿼리에 Multi Pattern의 개념을 적용한 것입니다. 앞서 말했듯이, 한 위치에 여러 객체가 존재할 수도 있습니다.
먼저, 기존 DETR이 구성한 초기 쿼리는 \( Q_f^{init} \in \mathbb {R}^{N_q*C} \)되고, 한 쿼리는 하나의 패턴인 \( Q_f^i \in \mathbb {R}^{1*C} \)을 포함합니다(i는 쿼리의 인덱스). 본 논문은 Multi Pattern을 학습하기 위해, 여러 패턴을 적용하여 하나의 쿼리를 \(Q_f^i \in \mathbb {R}^{N_p * C} \)로 재정의합니다(\( N_p \)는 패턴의 개수, 보통 3으로 설정).
그렇다면 Multi Pattern을 정의한 초기 쿼리도 \( Q_f^{init} \in \mathbb {R}^{N_qN_A*C} \)로 재정의됩니다. 마지막으로, 같은 앵커 위치에 Multi Pattern은 동일한 위치 정보를 공유함으로써, 앵커의 위치 정보도 \( Q_p \in \mathbb {R}^{N_pN_A * C} \)로 확장합니다(단순하게 앵커의 위치 정보 \( N_A * C \)를 \(N_p \) 만큼 반복시켜 줌).
그럼 이 초기 쿼리에 위치 정보를 더해, 최종적으로 Transformer Decoder의 입력으로 들어갈 쿼리가 만들어집니다.

그리고 최종적으로 Transformer Decoder의 출력에, 쿼리 \( Q_f \)를 다시 입력해 주어 Box를 예측에 대한 최적화를 가속시킵니다.

이러한 쿼리 덕에 좋은 성능과, 빠른 수렴 속도를 가지게 된 것을 실험으로 증명하였습니다.
Row-Column Decoupled Attention(RCDA)
마지막 제안 사항으로, 고 해상도로 올라갈수록 Attention 연산의 메모리 사용량이 기하급수적으로 증가하는 것을 줄이기 위해 RCDA를 제안하였습니다. 제안된 RCDA의 핵심은 Attention 연산을 전체 해상도에 대해 하는 것이 아닌, x축과 y축을 각각 독립적으로 연산하고, 마지막에 이 독립적인 Attention 연산을 결합해 주면 속도는 빠르고 비슷한 성능을 낸다고 본 논문에서 주장하는 바입니다. 이 Attention 연산을 진행하기 전에, 먼저 Query와 Key가 어떻게 구성되는지 살펴보겠습니다.


위 과정을 Transformer Decoder에서 Cross-Attention 연산을 예시로 들면, \( Q_f \)는 Object queries(\( \mathbb {R}^{N_q * C} \))가 될 것이고, \(K_f \)와 \(V_f \)는 Transformer encoder의 연산을 마친 Feature map(\( \mathbb {R}^{H*W*C} \))이 될 것입니다.
위 복잡한 수식을 간단하게 설명하면 \( Q_f \)와 \( K_f \)는 그대로 두고 여기에 대한 Position Embedding 값만 서로 다르게 넣어준다고 생각하시면 됩니다. 각각 위치 정보는 \( Q_f \)에서는 앵커의 좌표가, \( K_f \) Feature map의 각 해상도의 위치입니다. 이제 이 위치 정보에 대한 Position Encoding 함수를 구성하는데, x, y 중 하나의 좌표를 입력받는 \( g_{1D} \)를 구성합니다.
이렇게 함으로써, \( Q_f \)는 \( Q_x, Q_y \)가, \( K_f \)는 \( K_x, K_y \)로 x, y 각각의 독립적인 쿼리와 키가 구성이 됩니다. 여기서 쿼리들은 가만히 두고, 키들을 x축과 y축에 대해 독립적으로 연산하기 위해 1D Global Average Pooling(GAP)를 진행합니다(이 부분이 핵심입니다). 이렇게 되면 \( K_x \in \mathbb {R}^{H * W * C} \)는 \( K_x \in \mathbb {R}^{W * C} \), \( K_y \in \mathbb {R}^{H * W * C} \)는 \( K_y \in \mathbb {R}^{H * C} \)로 차원 축소가 이루어집니다.
위와 같이 축소된 차원에서 Attention을 진행하니 당연하게 메모리에 대해 효율적일 수밖에 없고, 성능은 오히려 증가했다고 합니다. Attention은 독립적으로 진행하고(\(A_x, A_y\)), 이후, 각각의 weighted_sum으로 두 연산을 결합해 주어 최종적인 출력이 이루어집니다(\( Z, Out \)).

마치며
이상 Anchor DETR의 포스팅을 마치겠습니다.
긴 글 읽어주셔서 감사합니다.
'컴퓨터비전 > Object Detection' 카테고리의 다른 글
| [논문리뷰] DAB-DETR (0) | 2024.04.07 |
|---|---|
| [논문 리뷰] Denoising DETR(DN-DETR) (0) | 2024.04.04 |
| [논문 리뷰] Conditional DETR (0) | 2024.03.29 |
| [논문 리뷰] Deformable DETR (0) | 2024.03.28 |
| [논문리뷰] DETR: End-to-End Object Detection with Transformer (0) | 2024.03.22 |




댓글