들어가며
본 논문은 Object Detection과 Transformer의 사전 지식이 있다는 가정하에 작성되었습니다.
오늘 리뷰할 논문은 DETR입니다. 이 논문은 Object Detection에 Transformer를 적용시킨 최초의 논문입니다. 그래서 이후에도 이 논문을 기준으로 Transformer를 Object Detection에 적용한 후속 연구가 많이 이루어졌습니다.
먼저 기존에 주로 사용되었던 2-stage Object Detection인 Faster R-CNN과 어떻게 변했는지 살펴보기 위해, 아래 Faster R-CNN 네트워크를 가져왔습니다.

위의 Faster R-CNN 같이 기존 Object Detection 모델은 최종출력 후에 중복된 박스를 제거하는 후처리(NMS) 과정이 필요합니다. 또한 각 박스를 예측하기 위해 Anchor Box와 같은 사전 정의도 필요합니다.
본 논문에서는 이러한 Hand-design component(Anchor, NMS)를 모두 없애고 End-to-End로 학습이 가능한 방법을 Transformer를 활용하는 새로운 방법을 제안하였습니다.
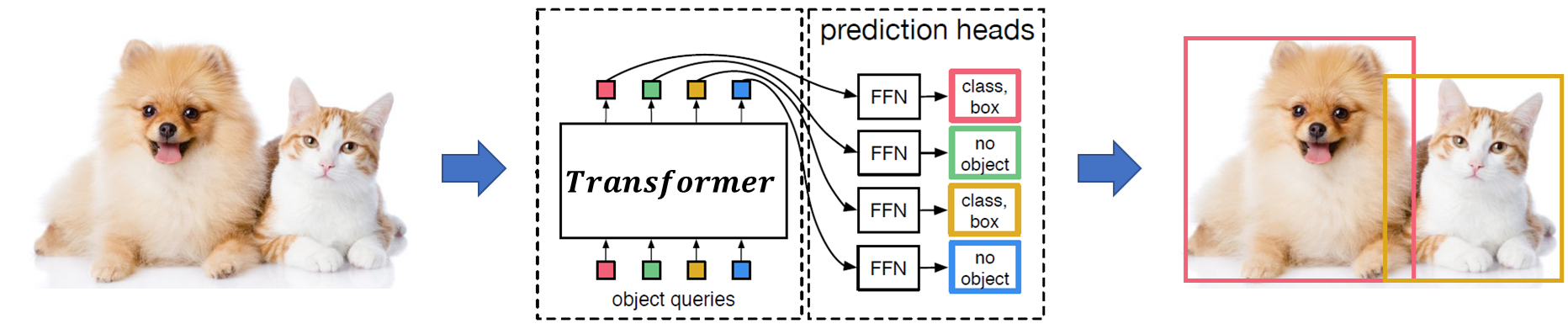
이 방식에서는 이미지 내의 객체들을 식별하기 위해 고정된 수의 Queries를 Transformer에 입력합니다. 각 쿼리는 이미지 내의 특정 객체(예: 강아지, 고양이)와 일대일로 Matching 되며, 해당 Object의 Class와 BBox(Bounding Box)를 예측하게 됩니다. 이러한 일대일 대응 구조 덕분에, 하나의 객체에 대해 단 하나의 쿼리만이 할당되므로 객체의 중복 예측 문제가 자연스럽게 해결됩니다.
더불어, Transformer 내부의 Attention 메커니즘은 입력된 쿼리들 사이의 상호 작용을 통해 유사한 객체에 대한 중복된 박스를 효과적으로 식별하고 제거하도록 모델을 학습시킵니다. 이는 모델이 이미지 내의 모든 객체를 정확하고 효율적으로 탐지할 수 있게 하는 핵심 요소입니다.
전체적인 개요는 이렇고, 그럼 이제 세부적인 구조를 살펴보도록 하겠습니다.
DETR Architecture
네트워크의 전체 구조는 아래와 같습니다.

크게 Backbone, Transformer Encoder-Decoder, FFN 3가지로 나눌 수 있습니다.
Backbone
먼저 Image에서 콤팩트한 Feature representation을 추출하기 위해 CNN Backbone을 삽입하였습니다.
입력 이미지 \( x_{img} \in \mathbb {R}^{3 * H_0 * W_0} \)가 CNN Backbone(e.g. ResNet)에 입력되어 저 해상도의 feature map \( f \in \mathbb {R}^{C*H*W} \)을 생성합니다(\( C=2048 \) and \( H, W = \frac {H_0} {32}, \frac {W_0} {32} \)).
Transformer encoder
위에서 출력한 feature map \( f \)를 Transformer 입력에서 계산량을 줄이기 위해 1 * 1 Convolution으로 차원 축소를 합니다(\( z_0 \in \mathbb {R}^{d * H * W}, d = 256 \)). 그리고 Transformer는 Sequence의 데이터를 입력으로 받기 때문에 \( d * HW \)로 Flatten 해줍니다.
그 후, 기존 Transformer와 동일하게 Positional encodings(상수)를 입력해 주고, Multi-Head self-attention과 Feed Forward Network(FFN)를 거칩니다.
Transformer decoder
충분히 큰 값을 가지는 고정 Query의 개수(\( N \))로 embedding을 설정합니다. 여러 데이터 셋을 보았을 때 한 이미지의 최대 객체수는 50 정도이므로, 보통 \(N \) 은 넉넉하게 100 정도로 잡아줍니다. 이 Embedding은 Transformer encoder의 출력과 Attention을 하기 때문에, 차원도 \( d \)로 맞추어 \(N * d \) 차원의 Input Embedding을 가집니다.
이 Input Embedding에는 Positional encodings이 입력되는데 여기서는 고정된 상수의 값이 아닌 학습가능한 Position 정보를 넣었답니다. 아마 Gt Object와 매칭되는 Object queries가 계속해서 변하면서 학습이 이루어지니, Position 정보도 학습이 가능하게 넣었지 않을까 하는 개인적인 생각입니다(아니면 그냥 실험으로 성능이 더 잘 나와서 그랬을 수도).
이렇게 Position 정보까지 입력된 Embedding은 Transformer encoder에서 출력된 Feature와 Cross-Attention으로 연산이 이루어집니다.
Feed-Forward Networks(FFN)
Transformer Decoder에서 출력된 Queries는 각각 독립적으로 FFN에 입력되어 각각의 Class(총 Class의 개수 + 1), BBox(center x, center y, width, height) 예측값을 출력합니다. 여기서 Class에 총 Class 개수보다 1을 더 더해준 것은, 전술한 바와 같이 \( N \) 개의 Queries는 GT의 객체 수 보다 충분히 큰 값이기 때문에 매칭되고 남는 Queries이 있을 것인데, 이 Class들을 no object(\( \phi \))로 설정하기 위해 +1을 해준 것입니다(기존 Object Detection의 Background로 해석).
그리고 각 Query의 Class들은 Softmax함수를 거쳐 확률값들을 출력하고, BBox의 값도 [0, 1] 범위로 정규화된 값입니다.
Loss
위 구조는 기존 CNN과 Transformer 구조를 그냥 결합한 형태로 보시면 됩니다. 이 부분이 본 논문의 핵심으로 제안하는 바입니다.
Bipartite Matching
본 논문의 핵심은 Transformer에서 출력된 Queries와 GT Objects를 1:1 Matching 하는 것입니다. 아까 \( N \)은 한 100 정도로 충분히 큰 값으로 설정했다 했죠? GT Object의 수는 무조건 이 값보다 작을 것입니다. 하지만 모든 Queries와 GT는 1:1 Matching이 되어야 하므로, GT도 나머지 공간에 \( \phi \)로 채워서 \( N \) 개로 맞춰줍니다. 그럼 최종적으로 아래와 같은 모양이 나오겠죠.
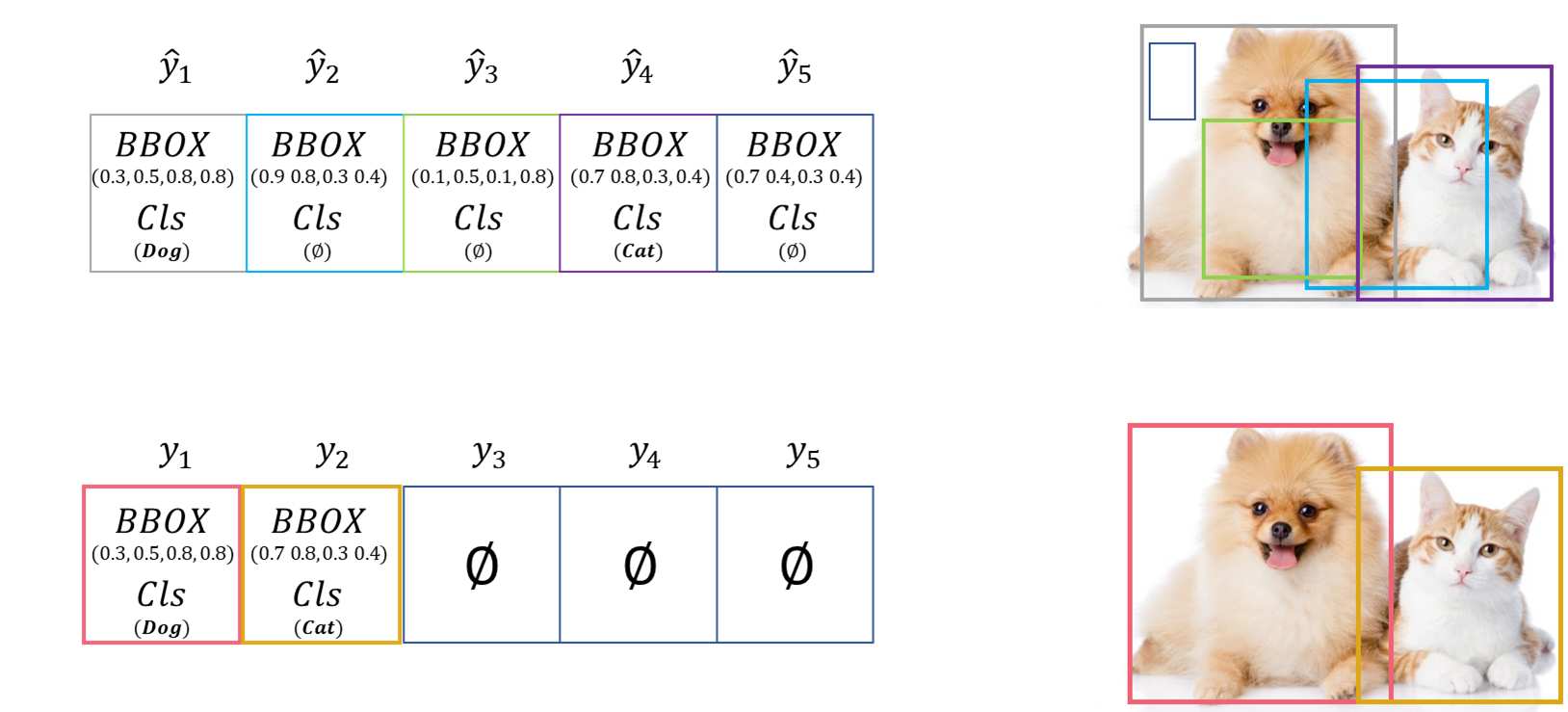
우리가 여기서 원하는 건 제일 매칭이 잘 되는 조합을 찾는 것입니다. 이를테면 \( \hat {y}_1 \)이 \( y_1 \)에 매칭되고, \( \hat {y}_4 \)가 \( y_2 \)에 매칭되고, 나머지는 알이서 no object로 매칭되면 최적일 겁니다.
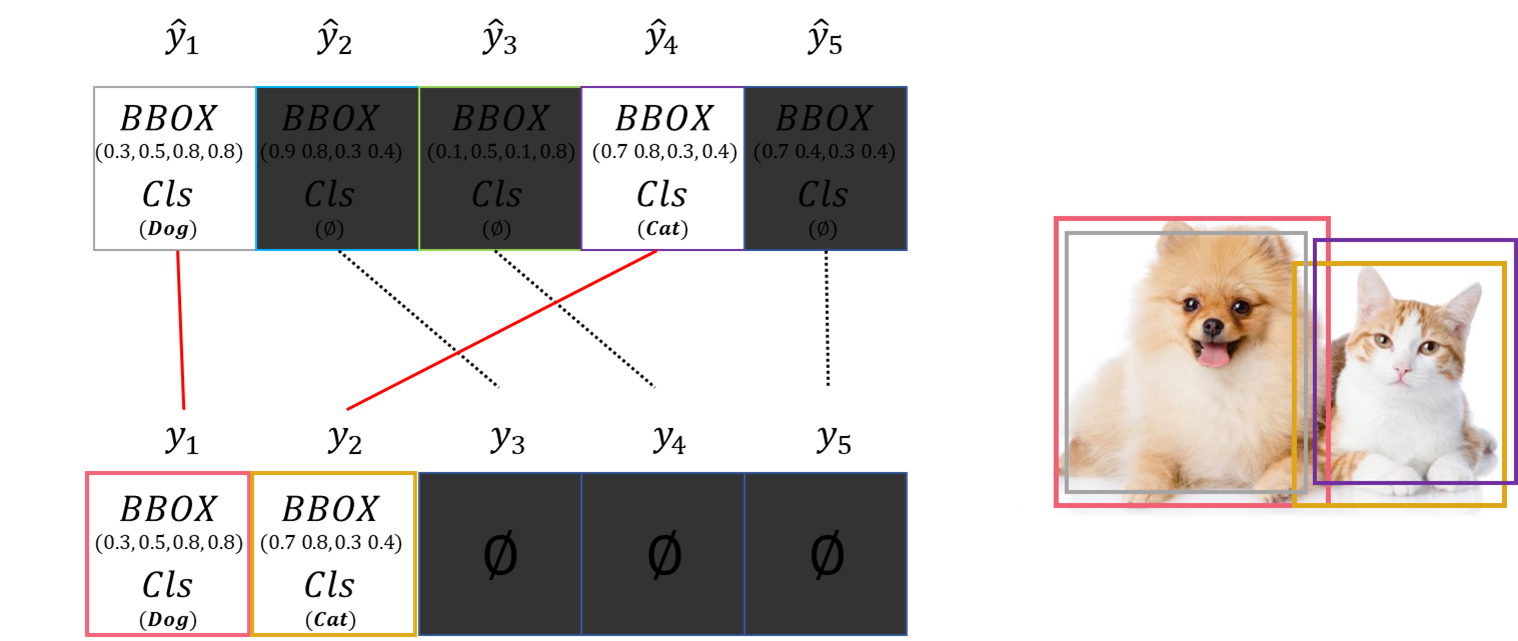
위의 조합이 Prediction과 GT 간의 최적의 조합입니다. 이 말을 풀어서 설명하면 Prediction과 GT 간 비용이 최소이가 되는 조합을 찾는 것으로 해석할 수 있습니다. 우리에게 주어진 정보(Class, BBox)로 Prediction과 GT의 비용 차이를 구하는 함수는 아래와 같습니다.

위의 \( \mathcal {L}_{box} \)는 전반적으로 사용하는 BBox에 대한 loss 함수입니다(자세한 설명은 생략합니다). \( \sigma \)는 GT와 Prediction의 조합입니다. 이렇게 비용 함수 \( \mathcal {L}_{match} \)를 구성하면 비용이 행렬형태로 나옵니다.
| \( y_1 \) | \( y_2 \) | \( y_3\) | \( y_4 \) | \( y_5 \) | |
| \( \hat {y}_1 \) | 1 | 9 | \( \phi \) | \( \phi \) | \( \phi \) |
| \( \hat {y}_2 \) | 10 | 8 | \( \phi \) | \( \phi \) | \( \phi \) |
| \( \hat {y}_3 \) | 4 | 15 | \( \phi \) | \( \phi \) | \( \phi \) |
| \( \hat {y}_4 \) | 10 | 2 | \( \phi \) | \( \phi \) | \( \phi \) |
| \( \hat {y}_5 \) | 9 | 7 | \( \phi \) | \( \phi \) | \( \phi \) |
대충 이런 식으로 나오겠죠. 위 행렬에서 \( \sigma \)를 계속해서 바꿔가며 제일 작은 비용을 가지는 최적의 조합 \( \hat {\sigma} \)을 찾는 것입니다.

그러나, 단순하게 전체 조합을 구하고 연산을 해서 계속해서 비용이 최소가 되는 조합을 찾아나가면 시간이 엄~청나게 오래 걸립니다. 여담으로 이렇게 단순하게 전부 다 구하는 것이 브루트포스 알고리즘이라고 합니다. 이렇게 조합을 찾는 거는 시간이 너무 오래 걸리니, Hungarian Algorithm이라고 브루트포스 알고리즘에 비해 훨씬 빠른 알고리즘을 사용하여 매칭하였습니다. 따로 이 알고리즘에 대한 설명은 하지 않겠습니다.
그냥 조합을 찾는 것에 더 빠른 알고리즘을 사용했다 정도로 아시면 무방합니다. 그리고 이 \( \hat {\sigma} \)을 구하는 과정은 Loss 함수가 아니라, 학습에는 사용되지 않고 단순하게 비용을 최소로 하는 조합만을 구하는 것이니 학습에 활용된다고 착각하시면 안 됩니다.
그리고 이것은 우리가 따로 구 할 필요 없이, 아래 코드와 같이 scipy에 내장된 함수입니다.
from scipy.optimize import linear_sum_assignment
import torch
cost_matrix = torch.Tensor([[1, 9], [10, 8], [4, 15], [10, 2], [9, 7]])
indices = linear_sum_assignment(c[i])
print(indices) # [(array([0, 3]), array([1, 2])]
위 Cost 행렬을 그대로 집어넣으면 row index들과 column index들을 출력합니다. 그리고 no object \( \phi \)는 연산되지 않기 때문에 제외됩니다.
자 이렇게 해서 이제 최적의 조합 \( \hat {\sigma} \)을 찾았다면, 이 조합으로 학습을 진행합니다. Loss함수는 기존 Object Detection처럼 Classification에서는 cross entropy와 box loss는 전술한 것과 같이 \( \mathcal {L}_{box} \)를 사용합니다.

마치며
이렇게 네트워크 구성부터 학습까지의 포스팅을 마쳤습니다.
Transformer를 Object Detection에 처음 적용한 논문이므로, 그만큼 후속 연구도 많이 나왔습니다. 하지만 이 모델은 학습의 수렴이 너무 느리며(500 epoch), 작은 객체에 대한 Detection은 기존의 모델들보다 현저히 떨어집니다. 수렴 속도를 개선하는 후속 DETR논문도 많이 나왔으니 포스팅하도록 하겠습니다.
끝으로 긴 글 읽어주셔서 감사합니다.
'컴퓨터비전 > Object Detection' 카테고리의 다른 글
| [논문 리뷰] Denoising DETR(DN-DETR) (0) | 2024.04.04 |
|---|---|
| [논문 리뷰] Conditional DETR (0) | 2024.03.29 |
| [논문 리뷰] Deformable DETR (0) | 2024.03.28 |
| [논문리뷰] Cascade R-CNN (0) | 2024.03.18 |
| [논문리뷰] Exploring Plain Vision Transformer Backbones for Object Detection (0) | 2024.01.16 |




댓글