단층 퍼셉트론(Single Layer Perceptron) 이란?
가장 단순한 형태의 신경망이다.
Hidden Layer가 없이 Single Layer로 구성되었고, 입력 피처들과 가중치, Activation, 출력 값으로 구성되었다.

출력 = F(w0(절편) + w1*x1 +w2*x2 + w3*x3 + ..... + wn*xn )
가중치 합: 입력 feature들의 개별 값과 이 개별 feature에 얼마만큼의 가중치를 주어야 결정하는 가중치 값을 각각 곱하고 최종으로 더해서 나온 값
출력 = 가중치값에 Activation 함수를 적용한 값
학습방법
값과 실제값의 차이가 최소가 되는 weight 값을 찾는 과정이 퍼셉트론이 학습하는 과정
퍼셉트론이 학습하는 것은 최적의 W벡터[w0, w1, w2, w3 ..., wn]의 값을 찾는 것이다.
1. 최초의 Weight값 설정
2. 설정된 Weight값과 입력 feature X값으로 예측 값 계산
3. 예측 값과 실제 값의 차이 계산
4. 예측 값과 실제 값의 차이를 줄일 수 있게 Weight값 변경
2, 4번 과정을 최적의 값을 찾도록 반복(경사하강법을 이용)
회귀

선형 회귀 모델로 예시를 들면, 최적의 회귀 모델을 만든다는 것은 잔차(오류 값)의 합이 최소가 되는 것이다.
오류 값이 최소가 되면 회귀 계수도 최적이란 이야기 이다.
RSS라고 오류의 값의 제곱을 구해서 더하는 방식이 있다. 제곱을 하는 이유는 나중에 미분을 더 편하게 하기 위함이다.
MSE는 RSS / N 이다
RSS = (y1 - (w1*x1 + w0)²) + (y2 - (w1*x2 + w0)²) + (y3 - (w1*x3 + w0)²) + ....(yn - (w1*xn + w0)²)
MSE = ((y1 - (w1*x1 + w0)²) + (y2 - (w1*x2 + w0)²) + (y3 - (w1*x3 + w0)²) + ....(yn - (w1*xn + w0)²)) / N

회귀에서 이 MSE는 비용이며 w변수로 구성되는 MSE를 (비용 함수, 손실 함수) 라고도 한다.
경사 하강법(Gradient Descent)
경사 하강법의 사전적 의미에서도 안수 있듯이, '점진적으로' 반복적인 계산을 통해 W 파라미터의 값을 업데이트 하면서 잔차의 값이 최소가 되는 W 파라미터를 구하는 방식이다.

위에서와 같이 젤 밑에 기울기가 최소가 되는 지점이 잔차가 최소가 되는 지점이다. 손실함수에서는 각 가중치마다 편미분을 해주어 미분 함수의 최솟값을 구해주어야 한다.
일반적인 1차함수로 예시를 들면
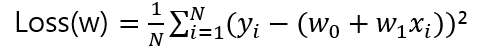
w1은 xi 값에 대한 가중치이고 w0은 절편이다. 여기서 각각 w에 대해 편미분 해주면 아래와 같은 식이 나온다.
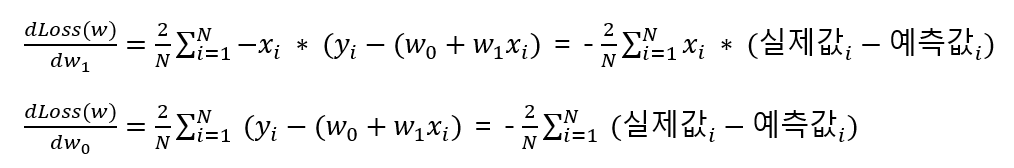
이렇게 기존 W값에 손실 함수의 편미분 값을 감소 시키는 방식을 적용하는데 일정한 계수를 곱해서 감수 시키며, 이를 학습률(Learning Rate) 이라고 한다.
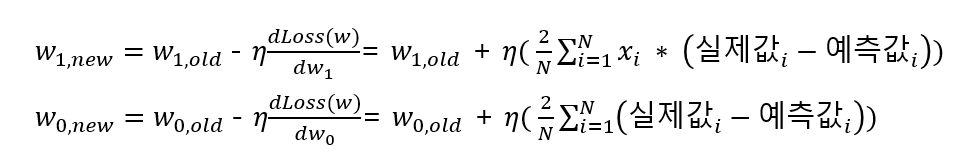
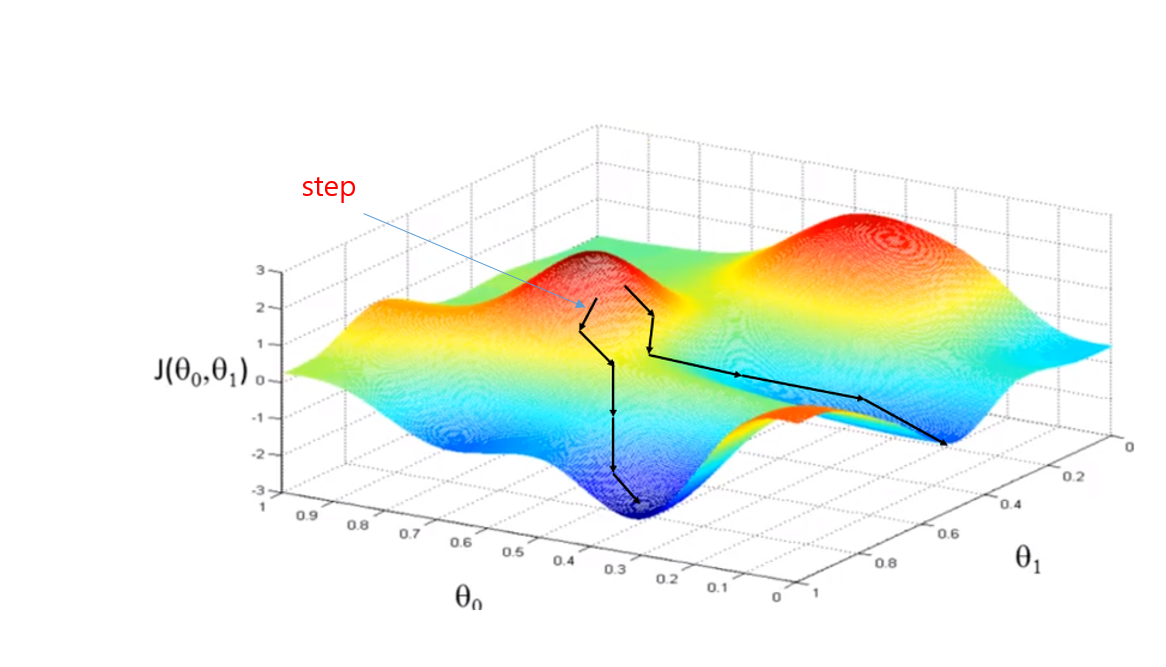
learning late 가 너무 작으면 step의 보폭이 짧아 너무 오래걸린다. 반대로 너무 크면 보폭이 너무 커 최소점을 찾지 못하거나 발산할수 있다.
'컴퓨터비전' 카테고리의 다른 글
| [딥러닝] 딥러닝의 Optimizer (0) | 2022.03.08 |
|---|---|
| [딥러닝] 딥러닝의 손실 함수 (0) | 2022.03.08 |
| [딥러닝] 활성화 함수( Activation Function) (0) | 2022.03.08 |
| [딥러닝] 다층 퍼셉트론(Multi Layer Perceptron)의 개요 (0) | 2022.03.06 |
| [딥러닝] 딥러닝의 개요 (0) | 2022.03.05 |




댓글