다층 퍼셉트론(심층신경망) 구조
심층 신경망(Deep Nueral Nerwork, DNN)은 입력층과 출력층 사이에 여러 개의 은닉층들로 이뤄진 인공신경망(ANN)이다. 기존 단층 퍼셉트론은 간단한 문제만 해결이 가능하고 더 복잡한 비선형 문제의 해결을 위해서는 은닉층(Hidden Layer)가 포함된 다중 퍼셉트론으로 심층 신경망을 구성하여야한다.


학습방법
1. Feed Forward를 수행. (단층 퍼셉트론와 마찬가지로 Input Layer와 Hidden Layer들의 가중치의 곱의 합에 Activation으로 Output Layer를 도출해낸다.)
2. 오차 역전파(Backpropagation)으로 뒤에서부터 거꾸로 가중치를 업데이트한다.
3. 1, 2 번 과정을 반복한다.

오차 역전파(Backprpagation)

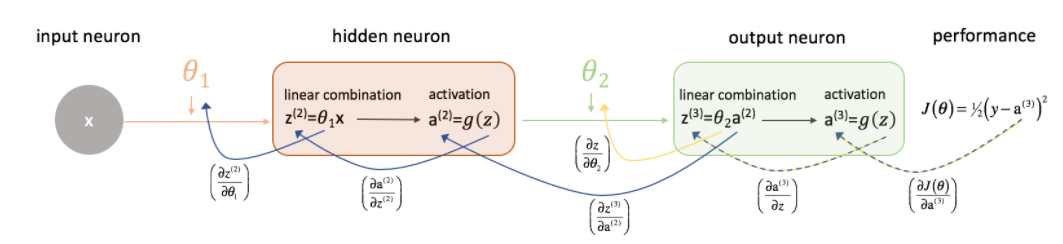
위와 같이 간단한 1개의 input, hidden, output으로 구성된 뉴럴 네트워크가 있다. 각각 가중치의 합에 Activation(f)을 한값이다. 밑의 그림을 보면 위의 식을 더 풀어서 설명한 것이다.

z(²) 는 θ1의 가중치 * x이고, a(²) 는 z(²)에 Activation을 한 값이다.
z(³) 는 θ2의 가중치 * a(²)이고, a(³)는 z(³)에 Activation을 한 값이다.
여기서 Backpropagation 으로 뒤에서 부터 거꾸로 가중치를 업데이트 하면 먼저 θ2의 가중치를 구해야한다. 먼저 최종 손실함수는 J(θ) = 1/2 * (y - a(³))² 이다. (1/2을 해주는 이유는 값이 너무 커지는것을 막기 위함이다. 무시해도 무방함.)
여기서 θ2의 가중치를 구하고 싶으면 J(θ)를 θ2로 미분해주면된다. 그럼 어떻게 미분을 해야할까?미분의 연쇄법칙으로 식을 추론해보면

이런 식이 나온다. 여기서 J(θ)는 a(³)함수이고 또 a(³)함수는 g(z)로 내부에 z함수가 있어 간단한 합성함수의 미분의 공식을 보면 f(g(x))를 미분하면 f'(g(x)) * g'(x)이다. 그래서 이 법칙을 적용하면

위와 같은 식으로 도출할수있다. 마찬가지로 이런 미분의 연쇄법칙을 적용해보면, θ1도 쉽게 구할수있다.

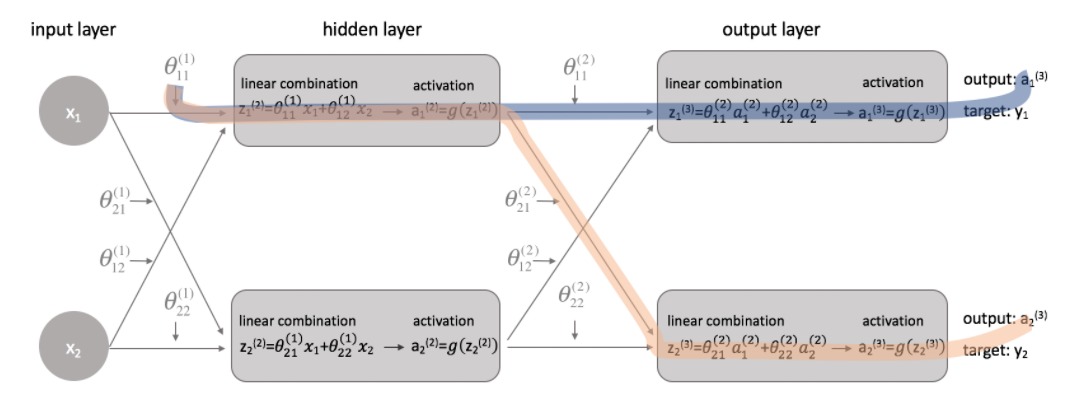
위와 같은 심층 신경망에서 θ(¹)11의 가중치를 구하려고하면 θ(¹)11의 가중치가 연결된 hidden layer는 θ(²)11와 θ(²)22 둘다 연결되어있다. 그러므로 θ(¹)11의 가중치를 구하고 싶으면 오렌지색과 블루색의 가중치를 backpropagation으로 각각 구해서 더해주어야 한다.
orange color:
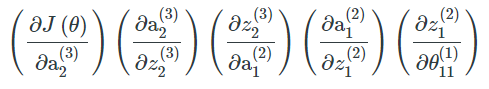
blue color:
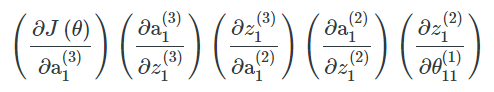
sum color:
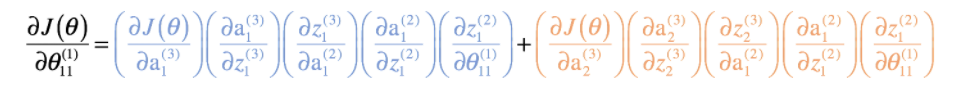
위와같은 방법으로 모든 레이어의 파라미터를 구하면 밑과 같은 식들이 나온다.

'컴퓨터비전' 카테고리의 다른 글
| [딥러닝] 딥러닝의 Optimizer (0) | 2022.03.08 |
|---|---|
| [딥러닝] 딥러닝의 손실 함수 (0) | 2022.03.08 |
| [딥러닝] 활성화 함수( Activation Function) (0) | 2022.03.08 |
| [딥러닝] 단층 퍼셉트론(Single Layer Perceptron)의 개요 (0) | 2022.03.05 |
| [딥러닝] 딥러닝의 개요 (0) | 2022.03.05 |




댓글