[논문리뷰] Information Maximizing Generative Adversarial Networks (InfoGAN)의 이해

InfoGAN 논문 링크

InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets

 

GAN의 이해 링크

[딥러닝] Generative Adversarial Nets(GANs)의 이해

상호 정보의 이해 링크

[통계] 상호 정보량(Mutual Information)

 

참조

https://datascienceschool.net/02%20mathematics/07.06%20%EC%A1%B0%EA%B1%B4%EB%B6%80%EA%B8%B0%EB%8C%93%EA%B0%92%EA%B3%BC%20%EC%98%88%EC%B8%A1%20%EB%AC%B8%EC%A0%9C.html

https://github.com/sungreong/Infogan/blob/master/img/lemma5.1.jpg

https://jaejunyoo.blogspot.com/2017/03/infogan-2.html

https://haawron.tistory.com/10#pf

https://vuetifyjs.com/en/api/v-calendar/#functions

 

소개

 

$InfoGAN$은 완전한 비지도 학습으로 $latent$ $variable(c)$을 학습할 수 있는 모델입니다. 분리된 표현이란 이미지의 회전, 두께 등의 기능을 의미합니다. 기존 $GAN$ 모델은 $Generator$에 $latent$  $code(z)$ 값만 들어가 이미지를 생성했습니다.  하지만 $InfoGAN$은 $latent$  $code(z)$에 $latent$ $variable(c)$를 추가하여 $G(z,c)$ 형태로 만들어집니다.

 

여기서 z와 c의 Mutual Information(MI)를 최대화시켜, 기존 $GAN$ 과는 차별화된 모습을 보여줍니다.

 

Mutual Information

$I(X;Y)$가 X, Y의 Mutual Information(MI) 이고, H(X), H(Y)는 각각의 엔트로피 값입니다. 이 엔트로피의 교차하는 지점이 MI가 되는 것이죠. 

 

InfoGAN RESULT

a, c, d는 InfoGAN으로 각각의 $z$에 유의미한 $c$ 값을 넣은 결과 입니다. 잘 나온 것 같죠? 그럼 이제 이 것이 무엇인가 천천히 살펴보도록 하겠습니다.

 

GAN과 InfoGAN의 차이

GAN의 수식

위는 기존 GAN모델의 수식입니다. 노이즈 벡터 z만 사용하고, 이 값은 맘대로 지정해도 됩니다. 그럼 사물이 회전하거나, 두께가 넓어지는 등의 데이터를 생성하기 위해선 어떻게 해야 할까요? 

 

 

위와 같은 그림이 있습니다. 오른쪽을 보고 있는 그림이 서서히 왼쪽을 보고 있는 그림으로 바뀌고 있죠?? 이 것은

처음 $lef{t}_{n}oisez$ 의 값을 서서히 조정하여 $righ{t}_{n}oisez$의 값에 도달하게 하면 됩니다. 그럼 여기서 문제가 생기죠. 과연 이 z에서 회전하는 의미를 가진 무언가를 찾을 수 있을까? 정답은 No겠죠? 처음 $noizez$의 값은 맘대로 지정했기 때문에 아주 얽힌 상태로 되어있습니다. 

 

여기서 이런 생각을 하는 사람도 있을 겁니다(물론 제가 그랬습니다...ㅎㅎ). 처음 왼쪽 이미지의 z값을 왼쪽 끄트머리 값만 높게 주고, 오른쪽 이미지는 오른쪽 끄트머리 값만 올려주면 되는 것 아닌가? 물론 좋은 아이디어입니다. 하지만 MNIST를 예시로 들었을 때, 2개의 샘플 1과 5가 있다고 가정해봅시다. 이 두 개는 독립된 데이터고, 각도 두께 등이 아예 다르죠? 이것을 하나의 $noizez$로 표현하는 것은 불가능합니다. 그래서 잠재 변수(c)를 사용하여 c의 기능만으로 회전이 이나 두께 등의 조절이 가능하게 한 것이죠.

 

http://jaejunyoo.blogspot.com/2017/03/infogan-1.html

위 그림을 보시면 위가 GAN이고 아래가 c를 추가한 InfoGAN입니다. 위는 엄청 꼬여있어서 어디로 이동해야 어떻게 될지 감이 안 잡히지만, 아래는 정돈된 상태라 위로 값을 수정하면 색깔이, 오른쪽으로 이동하면 뭐 두께가 바뀌는 등의 기능을 할 수 있다는 거죠. 자 그럼 이제 InfoGAN을 차근차근 파헤쳐 보도록 하겠습니다.

 

InfoGAN이란?

 

아까 말씀드린 것처럼 잠재 코드 z에 잠재 변수 c를 추가하여 학습한다고 말씀드렸습니다. 이러한 형태들이 모두 비지도 학습만으도로 이루어질 수 있다는 점이 아주 신기합니다... 자 그럼 어떻게 해야 할까요? 단순히 G(z)에 G(z, c)를 추가하여 학습하면 될까요? 그렇게 된다면 $P_G(x|c)=P_G(x)$를 만족하는 solution을 찾는 것으로 c의 가중치를 엄청 낮게 학습하여, 무시할 수도 있다네요.. 이런 사소한 문제에 대처하려고, 정보 이론으로 접근하여 상호 정보량(Mutual Information, MI)을 높도록 제약을 부여하는 것입니다. 아래는 정보이론 공식입니다. 증명은 맨 위 링크를 타고 보시길 바랍니다.

 

Mutual Information

$I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)$

 

Mutual Information은 X, Y 두 분포가 독립이거나, 종속일 때 사용하는데 어떻게든 c와 G(z, c) 간의 종속 구조를 만들어 보려고 MI를 도입한 것으로 보입니다. c의 분포는 어떻게 생겼는지 아무도 모르기 때문에 직접적으로 접근할 수 없고 apporximation(근사) 하는 방법으로 진행을 해야 한답니다. 

 

$I(X;Y)$ 상호 정보량입니다. 말 그대로 Y가 관측됐을 때 X의 불확실성 감소입니다. 즉, Y의 분포가 X를 잘 알면 알수록 값이 올라가고, 모르면 모를수록 불확실하니까 값이 내려갑니다. 그럼 여기서 X, Y가 독립이라면?? 아예 모르는 사이니까 0이 나옵니다. 이해가 좀 되시나요?

 

Variational Mutual Information Maximization

처음에 그냥 G(z, c)로 학습한다면 $P_G(x|c)=P_G(x)$를 만족하는 solution으로 c의 가중치를 엄청 낮게 학습해 c가 무의미한 값을 가진다고 했습니다. 그럼 의미 있게 학습하려면 위에서 Generator로 만들어낸 이미지와 c의 MI를 높게 걸어주면 된다고 말하고 있습니다. 즉, $I(C;G(z,c))$를 최대로 만들어주면 됩니다. 

 

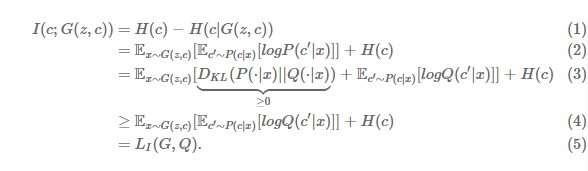
위의 MI의 공식과, 조건부의 엔트로피를 구하는 공식으로 (1), (2) 번은 이해했습니다. 하지만... (3) 번에서 처음 보는 무언가 등장했네요... 일단 H(c)는 고정적인 상수값이므로 제외하고 생각합니다. \( D_{KL} |)은 KL_Divergence인데 왜 이런 식이 나왔을까요? 해답은 P(c|x)에서 있습니다. 위에서 말했지만, c의 분포를 어떻게 생겼는지 모른다고 했고, p(x)의 직접적인 값을 얻기가 어렵습니다.

 

그래서 p(c|x)를 q(c|x)로 approximation(근사)할 수밖에 없습니다. 근사하는 과정에서 P와 Q사이에 약간의 괴리가 생기는데 이 괴리가 KLD의 최솟값인 0이 되면 (4) 번의 식이 성립합니다. 이 모델에 목표는 직접적인 값을 얻기가 힘드니까 근사한 모델에 $L1(G,Q)$의 lower bound를 최대로 올려주면 MI가 최대가 됩니다.

*수식 유도는 (2) 번 수식에서 log안에 $P(c^{\prime }|x)$에 $Q(c^{\prime }|x)$를 나누고 곱하면 수식 유도를 할 수 있습니다. 

 

앞에는 KLD로 해결이 됐지만 여전히 뒤에 $P(c|x)$로 샘플링해야 하는 $c^{\prime }\sim P(c|x)$의 부분이 남아있는 것을 볼 수 있습니다. 이 부분도 직접적으로 구하기 힘드니까 근사하는 방법으로 택했습니다.

 

먼저 law of total expectation이라는 확률론에서 잘 알려진 공식을 살펴봅시다.

논문에는 이것을 더 일반화하여 사용하였고, 아래와 같이 수식으로 표현됩니다.

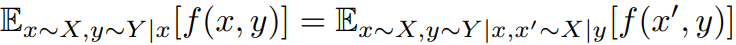
증명 출처: https://github.com/sungreong/Infogan/blob/master/img/lemma5.1.jpg

 

위의 식을 적용하니 $c^{\prime }\sim P(c|x)$ 부분이 없어지고, $L_I(G,Q)$의 계산이 Monte Carlo simulation으로 더 근사하기 쉬워진 것을 볼 수 있습니다.

 

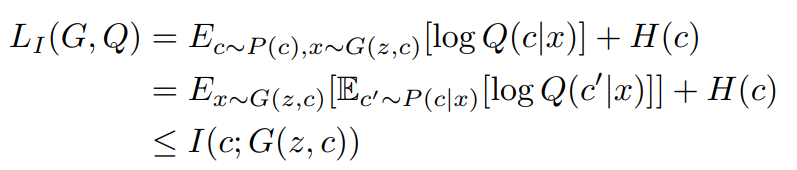
더 이상 $L_I$는 $P(c|x)$와 관련이 없고 우리가 다루는 G에 대해 Q를 최대화하는 문제가 해결이 되었습니다. 근사 분포 Q가 P에 완전히 가까워졌을 때 $L_I(G,Q)$가 $H(c)$로 최댓값을 가집니다. 즉, 근삿값이 직접적인 값에 도달했다는 의미이죠. 근사한 값은 lower bound라고 정의하였고, 이 과정에서 하한이 타이트해지고 최대 상호 정보량을 가질 수 있습니다.

 

기존 GAN의 학습 절차 변경 없이 GAN함수에 추가될 수 있고, 아래와 같은 식이 나옵니다.

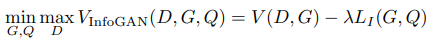
auxiliary distribution Q와 Discriminator D는 모든 Convolution Layer와 마지막 출력층인 Fully connected layer 공유합니다. 그래서 계산량 증가가 미미하다고 합니다. 

 

결과

 

이제 많은 개념을 살펴보았으므로, 처음으로 돌아와 MNIST의 결과를 살펴보겠습니다.

MNIST 결과

(a)를 살펴보시면, 2행 10열을 제외하고는 모두 잘 분류되었죠? (c)와 (d) 둘 다 -2에서 2까지 연속적인 값으로 이루어져서 연속적인 결과를 봅니다. (c)는 회전, (d)는 두께에 대한 결과가 부드럽게 변화된 것을 볼 수 있습니다.

 

Face Dataset

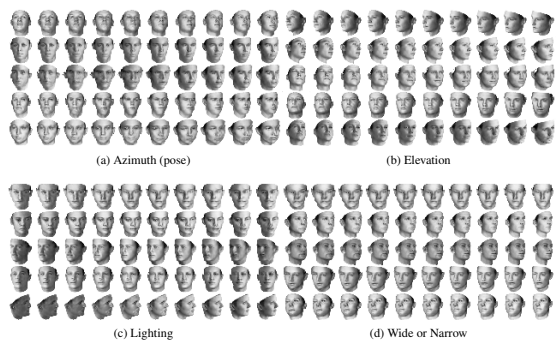
위 데이터는 비지도 학습으로 불가능한 데이터 세트입니다. 따라서 잠재 요인을 자동으로 발견할 수는 없었습니다. 하지만 InfoGAN의 경우 발견할 수 있다는 점이 놀라왔습니다. (b)의 경우 위에서부터 아래로 보는 방위를 부드럽게 표현했죠? (c)는 조명의 방향, (d)는 넓은 얼굴에서 좁은 얼굴로 잘 표현되었습니다.

 

 

(c)의 헤어스타일부터, (d)의 감정까지 표현이 된 것을 볼 수 있습니다.

 

다음에는 코드 구현으로 넘어가 볼까요.

긴 글 읽어주셔서 감사합니다.