소개
Generative Adversarial Networks
We propose a new framework for estimating generative models via an adversarial process, in which we simultaneously train two models: a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that
arxiv.org
Adversarial의 사전적 의미는 적대적이라는 뜻을 갖습니다. 말 그대로 두 모델이 대립하면서 동시에 학습시킵니다.
Fake Image를 만들어내는 Generator, 기존 진짜 이미지와 Generator로 만들어진 가짜 이미지를 평가하는 Discriminator 두 모델이 싸우면서 두 모델의 성능이 계속 올라가는 것입니다. G와 D가 정의되어 있기 때문에 다층 퍼셉트론으로 역전파 학습이 가능하게 되고, 마르코프 연쇄 등 복잡한 연쇄가 필요 없음을 증명합니다.
모델 목적

위와 같이 지폐 위조범(Generator)와 지폐 판별기(Discriminator)가 있다고 가정합니다. 이 지폐 위조범은 최대한 판별 기를 속여야 할 것이고 반면에 판별 기는 이 지폐가 Real인지 Fake인지 구별을 잘하여야 할 것입니다. 이 프레임워크의 목적은 판별기의 성능이 최대한으로 좋은 모델인데 여기서 지폐 위조범이 모두다 감쪽같이 속인다면 누구도 무엇이 Real인지 Fake인지 구별하지 못할 것이겠죠. 결과적으로 Real, Fake 모두 Real로 구별하여, 구별할 확률이 0.5에 이른 다는 것이 궁극적인 목표입니다.
\( Discriminator \) 모델은 \( Real\), \( Fake \)의 \( Label \)값을 알려주고 학습하는 지도 학습이고, \( Generator \) 모델은 \( latent code \)(잠재적 코드(노이즈))를 가지고 \( training \) 데이터가 되도록 학습하는 비지도 학습입니다. \( training \) 데이터가 되어야 진짜와 가짜를 분류하는 \( Discriminator \) 모델이 만들어지니까요.

위 그림을 보면 처음 \( lantent \)데이터가 \( Generator \) 모델을 통과하여 만들어진 이미지입니다. \( Epoch \)가 올라갈수록 육안으로 확인이 가능한 데이터가 만들어지고 있습니다.

\( Epoch \)가 올라갈수록 \( Generator \)모델이 \( Discriminator \) 모델을 잘 속이고 있어, 0.5로 수렴하는 것을 볼 수 있습니다.
학습 방법
위에서 말했듯이 \( D \)는 진짜데이터의 \(sample \) \( x \)를 \( D(x) = 1 \)로 학습하려 하고, \( noise \) \( z \)를 가지고 만든 \( G(z) \)에 대해서는 \( D(G(z)) \)로 학습하려 합니다. 그럼 \( D \)는 실수할 확률을 낮추려(mini) \( G \)는 \( D \)가 실수할 확률을 높이는 것(max)이 목표겠죠?그럼 아래와 같은 수식이 나옵니다.

\( x \sim P_{data} \)는 실제 데이터의 분포에서 샘플 \( x \)를 뽑은 것이고, \( z \sim P_{z} \)는 노이즈 분포에서 샘플 \( z \)를 뽑은 것입니다.
*기댓값(\( \mathbb{E} \))를 연산하는 방법은 모든 데이터를 하나씩 확인하고, 식에 대입한 뒤 평균을 계산하면 됩니다. 이산 확률변수와 연속 확률변수에 따라 계산방법이 달라집니다.
Discriminator가 아주 잘 판별하는 모델이라고 합시다. 그럼 당연히 실제 데이터에 대해서는 모두 1로 분류를 하여 앞의 항이 \( log 1 \)이 되어 제거될 것입니다. 뒤의 항도 노이즈 샘플이 Generator로 가짜 이미지를 만들어낸다 해도 0으로 분류를 할 것이고, \( log(1 - 0) \)이 되어 마찬가지로 제거될 것입니다. 이때 Discriminator의 입장에서는 최댓값을 얻습니다.
이제 Generator의 입장에서 한번 생각해볼까요?
*적대적 신경망이기 때문에 두 모델의 성능을 같이 끌어올려줘야 함
Generator는 진짜 데이터와 최대한 비슷하게 만들어 Discriminator를 속여야 하는 것인데, 그렇게 된다면 Discriminator는 어느 것이 진짜인지 가짜인지 구분하기 힘들어져, 0.5에 수렴한다고 위에서 말씀드렸습니다. 그럼 아래의 그래프도 쉽게 이해가 될 겁니다.

검은색은 data generating distribution\( (p_{data}) \), 파란색은 discriminative distribution \( (D) \), 초록색은 generative distribution \( (p_{g}) \)입니다. 위 그래프를 설명하기 앞서 하나의 이미지는 수많은 픽셀로 이루어져 있고, 그 하나의 이미지는 아주 높은 차원에서 하나의 점으로 표현할 수 있습니다. 위의 점들은 그 높은 차원의 점들의 분포입니다. 우리의 목표는 G로 만들어낸 이미지의 분포와 원래 이미지의 분포를 같게 하는 것입니다.
위 그림 맨 아래의 \( z \)가 \( G(z) \)로 매핑되어 \( x \)의 이미지를 만들어 냅니다. a에서 d 순으로 처음에는 파란점선이 실제 데이터에는 1에 가까운 결과를, 가짜 데이터에는 0에 가까운 결과를 도출하고 있습니다. 하지만 가면 갈수록 두 데이터의 분포가 비슷해지면서 마지막에는 진짜와 가짜를 구별해내지 못하는 0.5로 수렴하는 것을 볼 수 있습니다. 결국 \( P_{data} \)와 \( P_{g} \)가 같아진다고 보면 되겠네요.
결론적으로 \( P_{data} = P_{g} \) 일 때 Global Optimum을 가진다고 볼 수 있습니다.
증명
그럼 이제 알고리즘을 살펴보도록 하겠습니다.

Algorithm
- epoch의 수만큼 반복문을 수행
- 총 데이터 크기 // 배치 사이즈만큼 반복문 수행
- 배치 사이즈만큼 노이즈를 샘플링 \( p_{g}(z) \)
- 배치사이즈만큼 실제 데이터를 샘플링 \( p_{data}(x) \)
- \( D \)의 학습을 시작, 미니 배치만큼의 데이터의 loss를 구해 평균(m)을 구하고 \(\nablaθ_{d} \)만큼 학습률 곱함
- \( G \)의 학습을 시작, 미니 배치만큼의 데이터의 loss를 구해 평균(m)을 구하고 \(\nablaθ_{d} \)만큼 학습률 곱함
*D의 학습 목표는 앞 의항 \( logD(x) \)(실제 데이터 분류)를 모두 맞추고 뒤의 항 \( log(1 - D(G(z))) \) log(1 - D(G(z)))(가짜 데이터 분류)를 맞춰 loss가 0으로 목표
*G의 학습 목표는 \( log(1 - D(G(z))) \)(가짜 데이터 분류)를 모두 틀려 loss가 \( log(0) \) 즉 -무한대로 목표
- 여기서 앞 의항 \( logD(x) \)가 빠진 이유는 Generator 입장에서 Discriminator가 실제 데이터를 잘 맞추는지는 관심이 없음
증명하기 앞서서 \( p_{data} = p_{g} \) 일 때 Global Optimum을 가진다고 하였습니다. 진짜인지 하나의 가설을 세우고, 증명을 해보겠습니다.
Global Optimality of \( p_{g} = p_{data} \)
Proposition 1.
\( G \)가 고정되었을 때, 최적의 Discriminator는 아래와 같습니다.

Proof 1.
어떤 생성자 \( G \)가 주어졌을 때, \( D \)의 학습은 \( V(G, D) \)를 최대화하는 것입니다.

연속 확률분포이므로 위와 같이 식이 나오고, \(p_{z}(z) \)는 노이즈의 분포이고 \( G(z) \)는 Generator에 noize를 넣어 만든 이미지입니다. Discriminator의 이미지 분류를 목적으로 본다면, \( z \)를 \( x \)로 치환하며, \( g(z) \), \( dz \) 또한 \( x, dx \)로 치환되어 식이 나옵니다.
\( a = p_{data}(x) \), \( b = p_{g}(x) \), \( D(x) = y \)로 가정했을 시, 실수의 집합 0이 아닌 어떤 \( a, b \)에 대해 함수 \( y > alog(y) + blog(1-y) \)가 나오게 됩니다.

그래프로 표현하면 위 그림이 나오는데, 그러므로 구간은 [0, 1]이고, \( y = alog(y) + blog(1-y) \)을 미분하여 0이 되는 지점을 구하면 \( \frac {a}{a+b} = \frac {p_{data}(x)}{p_{data}(x) + p_{g}(x)} \)가 나옵니다. \(p_{data}(x) = p_{g}(x) \) 일 때 0.5이므로 성립하는 것을 알 수 있습니다. D의 목적함수는 \(p_{data}(x) = 1, p_{g}(x) = 0 \) 일 때 최솟값을 가지므로 다음과 같이 가상 학습 \( C(G) \)가 재구성될 수 있습니다.

Theorem 1.
우리의 목표는 다시 말해 \( p_{g}(x) \) = \( p_{data}(x) \) 이면 \( D_{G}^{*} = \frac {1}{2} \) 은 증명이 되었으니, 아래와 같은 수식이 나옵니다.

위 논문에서는 Kullback-Leibler divergence(KL)과 Jensen-Shannon divergence(JSD)를 제시하였습니다. 위키백과에 링크를 걸어두었으니 관심 있으시면 한번 보시길 바랍니다.
간단하게 설명하자면 KL은 두 확률분포의 차이를 계산하는 데 사용합니다. 서로의 정보 엔트로피를 계산하지만 비대칭으로, 두 값의 위치를 바꾸면 함숫값도 달라집니다. 그래서 거리를 계산해주는 함수는 아니지요. 이미지는 이산 확률변수이므로 아래와 같이 정의됩니다.

KL은 거리 개념이 아니기 때문에 두 확률 간의 분포 차이를 알기 위해서는 JSD를 사용해야 합니다. JSD는 두 확률분포의 유사성을 측정하는 방법입니다. 위와 함수와 다르게 대칭적이며 항상 유한한 값을 가집니다. 간단한 개념으로 KL의 순서를 바꾼 것 두 개를 구하고 평균을 얻는 방식입니다.
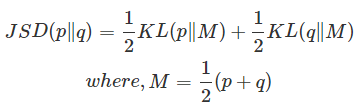
자 이제 두 개념을 알았으니, 논문에서 제시한 \( -log4 \)를 빼준 식을 보겠습니다.

JSD는 \( p_{data}, p_{q} \)가 같을수록 0에 가까워 집니다. 결과적으로 두 분포가 비슷할수록 \( -log(4) \) 에 수렴하는 것이 증명이 되었습니다.
Convergence of Algorithm 1
Proposition 2.
\( G \)와 \( D \) 가 충분한 용량을 가지고 있다면, 알고리즘 1의 각 단계에서 \( Discriminator \)는 주어진 \( G \)에 최적으로 도달하도록 허용되고, 그 기준에 부합하기 위해 \( p_{g} \) 가 업데이트됩니다.

이렇게 되면 \( p_{g} \)는 \( p_{data} \)로 수렴하는 것이지요.
Proof.
이제 이것이 사실인지 증명해보겠습니다. 증명하기 앞서 한 가지 사실을 알아야 합니다.
볼록 함수에서 최상부의 도함수 = 최댓값에 도달한 지점의 도함수
뭔가 당연한 소리 같죠?? 위 논문에서는 \( V(G, D) = U(p_{g}, D) \)로 바꿔 씁니다(단순히 바꿔 쓴 것이기 때문에 너무 신경 쓰지 마세요). 위의 말을 수식으로 풀어써보겠습니다.

*여기서 sup는 최상부를 의미하고, argsup는 최댓값의 지점을 의미합니다
만약 \( D \)는 \( p_{g} \)에 대해 최상부를 포함하고 있고 convex 함수라면, \( f_{D^{*}} \)(=최댓값의 지점)에서의 도함수는 최상부를 포함한 함수의 도함수와 같다고 제시합니다. 당연한 소리 같겠지만 \( G \)의 기준으로 편미분을 하면 앞의 항은 날아가고 \( log(1 - D^{*}_{G}(x)) \)만 남습니다. 그래프를 보시면 도함수 값이 0으로 수렴이 가능한 것을 볼 수 있습니다.

Thm1을 보시면 global optima가 \( -log4 \)로 증명이 되었습니다. 그래서 작은 업데이트 만으로도 \( p_{g} \)가 \( p_{data} \)로 수렴한다고 합니다. 우리는 \( p_{g} \) 자체보다 \( G(z; θg) \)를 최적화함에 있어 초점을 둡니다.
결론

위 이미지들을 보면 마지막에 바로 옆 이미지를 만들어 낸 것을 볼 수 있습니다. 그냥 복제한 것이 아닌 만들어 낸 이미지인 것을 알 수 있습니다. 비슷하게 잘 만들어낸 것을 볼 수 있습니다.
다음에는 코드 구현으로 넘어가 볼까요.
긴 글 읽어주셔서 감사합니다.
'컴퓨터비전 > GAN' 카테고리의 다른 글
| [논문리뷰] Information Maximizing Generative Adversarial Networks (InfoGAN)의 이해 (0) | 2022.11.18 |
|---|---|
| [논문리뷰] DEEP CONVOLUTIONALGENERATIVE ADVERSARIAL NETWORKS(DCGANs)의 이해 (0) | 2022.11.14 |


댓글