[논문리뷰] SETR: SEgmentation TRansformer

참조

 

[논문리뷰] AN IMAGE IS WORTH 16X16 WORDS:TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE(Vision Transformer)

 

 

들어가며

 

본 논문이 게재될 당시, 대부분 Semantic Segmentation은 Convolution layer의 Encoder-Decoder로 이루어져 있는 Fully-Convolutional Networks(FCN)로 구성되어 있었습니다.

 

위 구조에서 Encoder에서는 해상도를 줄여가면서 Convolution layer를 적용하여 다양한 Feature Representations을 학습해나갔고, Decoder에서는 학습된 Feature Representations으로 점차 해상도를 Upsampling 하여 Pixel-Level Class를 예측하였습니다.

 

FCN 구조는 당연히 Encoder에서의 Feature Representations 학습이 잘 되어야, Decoder에서의 복원도 잘 될 것입니다. 기존 Convolution Layer의 특성상 고정된 커널(e.g. 3*3, 5*5, 7*7)을 사용하여 수용필드가 제한적이기 때문에, FCN에서는 고정된 커널에 해상도를 점진적으로 줄여가는 전략으로 장기의존성을 늘려갔습니다.

 

하지만, 고정된 커널의 사이즈를 가지는 CNN에서 해상도를 줄여가며 층만 무작정 깊이 쌓아가면 어느 순간 성능이 더 이상 늘지 않고, 오히려 발산하는 한계에 봉착합니다. 따라서, 본 논문인 이러한 CNN 구조 자체가 장기 의존성이 거의 없다는 주장을 하고 있습니다. 

 

고정된 커널에서 장기의존성 문제

 

 

이러한 장기의존성은 단순 이미지 분류가 아닌, 전체 픽셀에 대한 클래스 분류를 해야 하는 Semantic Segmentation에서는 아주 중요하기 때문에 기존에는 수용필드를 늘리려고 Convolution의 변형인 Dilated Convolution, 피라미드 구조 등을 적용하여 좋은 성과를 내고 있었습니다. 

 

하지만 Encoder에서 해상도를 줄여가면서 Feature를 학습하고, Decoder에서 다시 해상도를 복원하는 기존 FCN의 구조는 탈피하지 못했다고 합니다. 본 논문은 이러한 지배적인 FCN 구조를 탈피하고, 장기의존성에 근본적인 문제를 가지는 CNN을 전부 Transformer로 변경한 SEgmentation TRansformer(SETR)을 제안하였습니다.

 

Transformer의 Attention 연산은 CNN과 달리 전역적인 수용필드를 가져 장기의존성에 강하고, 입력 해상도와 출력 해상도가 동일한 Sequence-to-Sequence 구조이니 FCN 구조를 탈피했다고 할 수 있습니다.  

 

자세한 구조는 아래에서 설명하겠습니다.

 

 

Segmetnation Transformers(SETR)

 

SETR의 전체구조는 아래와 같습니다.

 

 

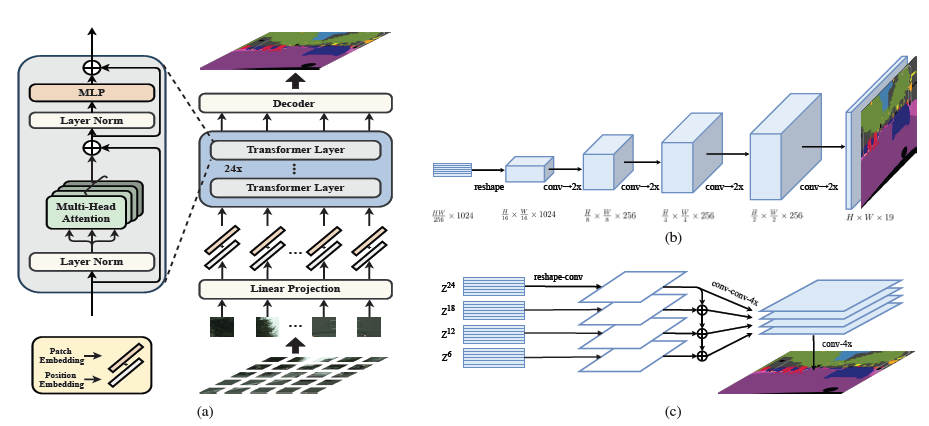
먼저 (a) Transformer Encoder는 Feature map을 Patch로 나누고 Self-Attention을 진행하는 구조로,  ViT와 동일한 구조입니다. 자세한 설명은 ViT 글을 참고해 주시길 바랍니다.

 

Decoder designs

 

본 논문에서 Transformer Encoder의 출력인 feature \( Z \)에 대한 Decoder의 디자인은 총 3가지를 제안하였습니다.

 

• Naive upsampling(Naive): 이름 그대로 아주 심플하게 구성된 Decoder입니다. 1*1 Convolution + batch norm(+ReLU) + 1*1 Convolution으로 네트워크를 구성하였으며, 최종 출력은 Class의 개수(e.g. COCO의 경우 80개)입니다. 이후, Bilinear interpolation으로 원래 이미지의 해상도를 복원하고 Cross Entropy로 loss를 구합니다. 
  
  
• Progressive Upsampling(PUP): Naive와 같이 단순하게 하나의 Convolution 네트워크를 구성하는 것을 넘어, FCN처럼 점진적으로 Convolution과 Upsampling으로 해상도를 늘립니다. 초기 Encoder의 출력이 1/16인 것을 감안하면, 4개의 연산이 필요합니다(위 그림의 (b)). 
  
  
• Multi-Level feature Aggregation(MLA): 위 그림의 (c)인데 feature pyramid와 구조적으로는 비슷하면서, 전체 출력 \( z^l \)이 Transformer Encoder에서 출력된 해상도 이기 때문에, 동일한 해상도를 가진다는 점에서 다릅니다.
  
  \( \frac {L_e} {M} \) 스텝마다 균등하게 Encoder에서 출력된 레이어들로 총 \( M \) 개의 출력 레이어들이 Decoder에 활용됩니다. 위 그림에서는 \( M = 4 \)이고, \( L_e = 24\) 이고, 절차는 아래와 같습니다.
  
  
  1. \( \frac {HW} {256} * C \)로 구성된 M개의 각각 레이어들을 \( \frac {H} {16} * \frac {W} {16} * C \)의 해상도로 Reshape 하고, 출력 채널이 반으로 줄어드는 1*1 Conv를 통과하여 \( \frac {H} {16} * \frac {W} {16} * \frac {C} {2} \) 차원을 출력.
     
     
  2. Top-Down 방식으로 행렬끼리 Addition을 해줌
     
     
  3. Addition 된 각각을 1. 출력 채널이 같은 3*3 Conv를 통과하여 \( \frac {H} {16} * \frac {W} {16} * \frac {C} {2} \) 차원을 출력하고, 2. 출력 채널이 반으로 줄어드는 3*3 Conv를 통과하여 \( \frac {H} {16} * \frac {W} {16} * \frac {C} {4} \)차원을 출력. 이후, 3. 4x bilinear interpolation을 진행하여 \( \frac {H} {4} * \frac {W} {4} * \frac {C} {4} \)차원을 출력.
     
     
  4. 마지막으로, M개의 Layer들은 각각 1. 채널을 기준으로 결합(concatenation)하여 \( \frac {H} {4} * \frac {W} {4} * C \) 차원을 출력하고, 2. 4x bilinear interpolation을 진행하여 최종 \( H * W * C \)차원을 출력.

 

마치며

 

오늘은 SETR 논문을 리뷰해 보았습니다.

긴 글 읽어주셔서 감사합니다.