Abstract
CNN은 유한 공간 범위의 local filters의 weights를 학습함으로써, 많은 효율성을 달성해왔다. 필터가 무엇을 보고 있는지는 알수있지만, 이미지의 위치는 알 수 없다는 제한점이 존재합니다. Absolute position에 관한 정보는 본질적으로 유용하다고 알려져있고, CNN이 이러한 정보를 인코딩하는 방법을 암묵적으로 학습할 수 있다고 가정하는 것입니다. 본 논문에는 일반적으로 사용되는 ResNet과 같은 신경망에 이 가설을 테스트합니다.
Introduction
CNN은 많은 분야에서 우수한 성적을 내고 있었지만, 이것을 딥러닝의 맥락에서 해석 가능성이 부족하다는 비판을 받고 있었습니다. 위치에 의존적인 작업(e.g. semantic segmentation, Object Detection)에 중요한 Alsolute spatial information을 가져오는지 불분명합니다.
아래 그림을 보면 이미지에서 가장 두드러지는 부분은 보통 중앙에 있습니다.

중앙에 두드러진 부분에 공간 정보가 잘 해석된 것을 볼 수 있습니다. 그렇다면 이러한 영역을 잘라서 두드러지는 부분을 오른쪽에 배치해도 이 공간 정보를 잘 해석할까요?
본 논문에서는 CNN이 feature map으로 부터 위치 정보를 인코딩 하는 것을 실제로 배울 수 있는 가설로 시작합니다. 그리고 positoin information이 명확하게 학습이 되어 지고, 이것은 기존 CNN에서 차원 유지를 위해 사용하던 zero-padding이 중요한 역할을 하였습니다. 이것은 단순 차원 유지만 하는 줄 알았지, 이러한 효과는 오래 전부터 숨겨져 있었다고 합니다. 이 연구는 CNN에서 학습된 feature의 본질을 더 잘 이해하는데 도움이 된다고 시사합니다.
CNN은 fully connected network의 엄청난 수의 weight를 대처하는 방법으로 처음 등장했습니다. 이 CNN에서 학습된 커널은 이미지의 아주 작은 부분의 feature만 학습이 이루어지고, 수많은 texture나 색깔에 의존했습니다. 그럼에도 불구하고, 위치 정보는 이미지에서 물체가 어디서 나타날지에 대한 강력한 단서이고, 이 단서는 네트워크의 feature안에 포함되어 있다고 생각합니다. 본 논문에서는 이 가설을 테스트하고, CNN이 실제로 공간 정보에도 의존하고 학습도 할 수 있는 증거를 제공합니다.
Position Informataion in CNN
CNN은 자연스럽게 초기 컨볼루션 단계에는 미세한 수준의 높은 Spatial-frequency details(e.g. edges, texture, lines 등)을 추출하려고 하고, 깊어질수록 카테고리에 따라 가장 풍부한 features를 추출합니다.
본 논문에서는 위치 정보가 이러한 feature map에서 암묵적으로 인코딩 되었을거라 가정하고, classification, object detection, semantic segmetation에 아주 중요한 역할을 한다고 합니다. 그래서 이 가정을 증명하기 위해 여러 실험을 진행합니다.
Position Encoding Network
본 논문은 위치 정보를 Position Encoding Network(PosENet)로 추출하고 여기에는 2가지 핵심 요소가 있습니다.
- feed-forward convolution encoder(\( f_{enc} \))
- simple position encoding module(\(f_{pem} \))
위의 인코더 네트워크는 서로 다른 레벨의 features를 추출하는 multi-scale layers 구조입니다. 그리고 position encoding module은 이 multi-scale features를 입력으로 받아, absolute 위치 정보를 예측하는 구조입니다. 아래는 전체 구조입니다.

- Encoder-
본 논문에서는 \( f_{enc} \)로 ResNet과 VGG를 사용합니다. 단, 마지막에 분류에 활용되는 average pooling과 fully-conntected network는 제외합니다. 여기서 각 feature를 추출하는 블럭들은 (\( f^1_{\theta}, f^2_{\theta}, f^3_{\theta}, f^4_{\theta}, f^5_{\theta} \))로 표기하고, 여기서 추출된 features는 (\( f^1_{pos}, f^2_{pos}, f^3_{pos}, f^4_{pos}, f^5_{pos} \)) 로 표기합니다. 본 논문에서는 이 Features로 위치 정보를 이끌어내야 하기 때문에 이 Weight들은 Frozen 됩니다.
- Position Encoding Module-
이 모듈에서는 인코더의 Features로 부터 위치 정보를 예측해야 하므로, 인코더에서 추출한 features인 (\( f^1_{pos}, f^2_{pos}, f^3_{pos}, f^4_{pos}, f^5_{pos} \))를 입력으로 받습니다. 이 features의 모든 해상도를 맞춰수기 위해 bi-linear 보간법을 시행하고 결합해줍니다.

이 결합된 feature map들에 k * k의 컨볼루션 연산을 합니다. k = {1, 3, 5, 7}의 후보가 있으며 나중에 비교 실험을 할겁니다.

위의 \( W^c_{pos} \)가 컨볼루션 연산이며, 아 Weight들은 학습할 수 있는 가중치입니다.
이 모듈의 주요 목적은 일반적인 분류에서 학습을 진행할 때, 위치 정보가 암묵적으로 학습되는지 여부를 검증하는 것입니다. 그래서, 이 모듈은 숨겨진 위치 정보와 Ground-Truth(GT) 마스크와 같은 gradient 사이의 관계를 모델링하는 것입니다. 이 위치 정보가 인코딩되지 않는다면 출력은 랜덤하게 출력될것입니다.
Synthetic Data And Ground-Truth generation
위치 정보의 존재를 평가하기 위해, 정규화된 Gradient와 같은 위치 맵을 아래 그림과 같이 GT( \( \mathcal {G}^h_{pos} \) ) 로 할당하여 randomization test를 구현합니다. 여기서 Gradient는 우리가 흔히 아는 역전파가 아니라, 픽셀의 강도를 의미합니다.

Absolute 위치의 GT 마스크는 Horizontal(H), Vertical(V), Gaussian distribution(G) 가 존재하고, 이 세 가지 패턴을 생성하는 핵심 동기는 모델이 한 축 또는 두 축의 절대 위치를 학습할 수 있는지를 확인하는 것입니다.
H는 왼쪽에서 오른쪽으로 갈수록 값이 증가, V는 위에서 아래로 내려갈수록 값이 증가, G는 구석에서 중앙에 가까워질수록 값이 증가합니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter
def generate_gradient_masks(rows, cols):
# 수평 그라디언트 마스크 생성
horizontal = np.tile(np.linspace(0, 1, cols), (rows, 1))
# 수직 그라디언트 마스크 생성
vertical = np.tile(np.linspace(0, 1, rows), (cols, 1)).T
# 가우시안 그라디언트 마스크 생성
x, y = np.meshgrid(np.linspace(-1, 1, cols), np.linspace(-1, 1, rows))
d = np.sqrt(x*x + y*y)
sigma, mu = 1.0, 0.0
gaussian = np.exp(-( (d-mu)**2 / ( 2.0 * sigma**2 ) ) )
return horizontal, vertical, gaussian
# 마스크 생성 예시
rows, cols = 100, 100
horizontal, vertical, gaussian = generate_gradient_masks(rows, cols)
# 생성된 마스크 시각화
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.imshow(horizontal, cmap='gray')
plt.title('Horizontal Gradient')
plt.subplot(1, 3, 2)
plt.imshow(vertical, cmap='gray')
plt.title('Vertical Gradient')
plt.subplot(1, 3, 3)
plt.imshow(gaussian, cmap='gray')
plt.title('Gaussian Gradient')
plt.show()
이 값들은 랜덤하게 적용되었다고 합니다. 왜냐하면 입력 이미지와 absolute 위치와는 상관관계가 없고 독립적이기 때문입니다. 그렇기 때문에 어떠한 데이터 세트를 선택해도 상관이 없습니다.
Training the network
본 논문은 사전 학습된 네트워크로부터 위치 정보를 인코딩하는 것을 목표로 하기 때문에, 모둔 실험에서 인코딩 네트워크 \( f_{enc} \)의 weight는 freeze합니다. 그리고 position encoding module인 \( f_{pem} \)는 최종적인 position map \(\hat {f}_p \)을 생성합니다. 그리고 이 \(\hat {f}_p \)를 gt position map 크기만큼 업샘플링 시켜주고, 픽셀별 mean squared error로 loss 함수를 구성합니다.

\( x \in \mathbb{R}^n \)과 \( y \in \mathbb{R}^n \)는 각각 predict(\( \hat{f}_p \)), GT( \( \mathcal {G}^h_{pos} \) ) 입니다.
Experiments
이 position encoding 측정은 보편적이지 않고 새로운 연구에 대한 방향입니다. Metrics으로는 Spearman Correlation(SPC)와 Mean Absolute Error(MAE)를 선정하였습니다.
스피어만 상관계수는 두 변수 간의 순위 기반 상관 관계를 측정하는 기법입니다. 위에서는 \( \hat{f}_p \)와 \( \mathcal {G}^h_{pos} \)가 두 변수입니다. 이 기법은 특히 비선형 관계에서 유용하다고 알려져있습니다.
- 데이터 순위 매기기(e.g. data = [3, 4, 5, 3, 2, 1, 7, 5]
- 정렬: [1, 2, 3, 3, 4, 5, 5, 7]
- 순위 매기기: [1, 2, 3.5, 3.5, 5, 6.5, 6.5, 8] (동일한 수는 순위의 평균을 매깁니다(e.g. 3, 3은 순위 3, 4위에 대응하므로 3.5위)
- 정렬: [1, 2, 3, 3, 4, 5, 5, 7]
- 순위 차이 계산: 각 픽셀간에 순위 차이를 계산 후 제곱합니다.
- 스피어만 상관계수 계산: 아래와 같은 공식으로 스피어만 상관계수(\( \rho \))를 계산.
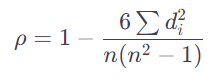
Position Information in Pretrained Models
본 논문에는 총 2가지 종류의 비교 실험을 합니다.
- 먼저 사전 학습된 모델(VGG, ResNet)로 position information를 가져올 수 있는지 검증
- 사전 학습된 모델의 사전 지식으로부터 position information이 유도되지 않는다는 것을 정당화하기 위해 PosENet을 학습하여 검증(패딩 없이 진행).

확실히 사전학습된 모델은 position information을 쉽게 추출할 수 있었지만, 그렇지 않은 PosENet은 낮은 성능을 기록하였습니다. 이러한 결과로 사전 학습된 모델 없이 position information을 이끌어 내는것은 어렵다는 결과가 나옵니다. 그리고 상대적으로 HS, VS에서 낮은 성능을 기록하는데, 기존 H 패턴 같은 경우에는 sine wave의 1/4로 볼 수 있지만, HS 및 VS 같은 패턴은 더 깊은 이해가 필요한 sine wave의 반복 주기로 간주될 수 있어서 그렇답니다. 아래는 다양한 패턴에 대한 상관계수 결과 입니다.

각각 H, G, HS 패턴인데, 모든 아키텍처에서 position informations이 암묵적으로 인코딩 된다는 처음 가설을 강력하게 입증하고 있습니다.
Analyzing PosENet
이 절에서는 두 가지 추가적인 실험을 진행합니다.
Impact of Stacked Layers
위 표는 이미지 분류에서 사전 학습된 모델에서 PosENet에 하나의 convolution layer로 position information을 추출한 결과였습니다. 하지만 숨겨진 position information을 더 정확하게 추출하기 위해 이 layer의 수를 늘려보았을 때 성능에 어떠한 영향을 미치는지 확인해보았습니다.

layer의 수를 늘리는 것이, 확실히 모든 모델에서 성능이 올라갔습니다. 이러한 큰 이유는, convolution layer의 층을 쌓는 것은, 더 크고 효율적인 receptive field를 제공해서라고 합니다. 예를 들면, 5*5 convolution layer와 2개의 3*3 convolution layers는 receptive field가 같다고 주장합니다.
Impact of varying Kernel Sizes
추가적으로 다양한 kernel sizes가 성능이 얼마나 미치는지 확인합니다.

위와 같이 더 큰 kernel sizes 일수록 성능이 증가하는 것도 확인할 수 있었습니다. 아래는 시각적인 비교 결과입니다.

Where is the position information stored?
이 절에서는 position information이 모든 레이어에 동등하게 분포되어 있는지 확인합니다. 사전학습 모델로는 VGG를 활용하였고, position encoding module에서는 하나의 convolution layer로 구성하였습니다.

위 결과를 보면 \(f^5_{pos} \)가 \( f^1_{pos} \)보다 월등히 높은 성능을 기록하였습니다. 이는 얕은 층보다 깊은 층이 더 많은 feature map이 추출된 결과로 볼 수 있습니다(512 vs 64개의 층). 이 결과로 보아, 더 높은 수준의 의미를 나타내는 깊은 층에서 positional information의 더 강력한 인코딩을 나타낼 가능성이 있다고 합니다. 그러므로 깊은 수록 더 많은 position information을 가진다고 합니다.
Where does position information come from?
본 논문은 convolution layer에서 입력과 출력 해상도를 맞추기 위해 주로 사용되었던 Zero-padding이 학습해야할 위치 정보를 전달한다고 합니다. 그래서 이 절에서는 사전학습된 VGG16의 모델에 모든 패딩을 삭제해보았고(ResNet은 skip connection 때문에 불가능), 또한 PosENet에 패딩도 삭제하여 성능에 어떠한 영향을 미치는지 확인해보았습니다.

모든 모델에서 padding이 있을 때 성능이 크게 향상된 것을 볼 수 있습니다. 아울러 padding이 2일 때, PosENet에서 명확하게 position information 역할을 한 것을 볼 수 있습니다. 아래는 이것을 시각화 한 것 입니다.

Case Study
이 절에서는 이미지안에 semantics가 position map에 어떤 영향을 주는지 확인합니다. 이를 시각화 하기 위해, content loss heat map을 계산합니다 .
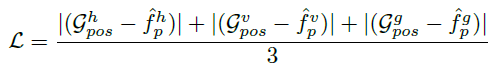
\( \hat {f}^h_p, \hat {f}^v_p, \hat {f}^g_p \)는 각각 horizontal, vertical, Gaussian의 position map 입니다. 아래 그림을 각각 모델에 대한 heatmap입니다.

맨 위에 행이 PosENet인데 모서리 쪽에 content loss가 더 큰 것을 볼 수 있습니다. 그리고 VGG, ResNet의 loss map은 이미지의 semantics와 더 상관관계가 있습니다. 특히, ResNet은 더 깊은 층을 쌓음으로써, 더 강한 연관성이 있습니다. 왼쪽 그림부터 오른쪽 그림까지, 얼굴, 사람, 고양이, 비행기, 꽃병 순으로 가장 loss가 큽니다. 이러한 시각화는 모델이 어느 지역에 초점을 맞추는지 보여주는 대안적인 방법이 될 수 있습니다.
Zero-Padding drived position information
추가적으로 semantic segmentation, object detection에서 position에 어떤 상관관계가 있는지 검증합니다. 먼저 VGG로 zero-padding 없이 처음부터 학습하여, object detection task의 공공데이터세트에 대한 평가를 합니다.

확실히 zero-padding을 포함하는 것이 성능 향상에 도움이 되었습니다.
또한 semantic segmentation에도 평가를 진행하였습니다.

다음은 각각 VGG(Image classification), VGG-SS(Semantic Segmentaiton), VGG-SOD(Object Detection)에 position information이 얼마나 작용하는지 비교 입니다.

object detection과 semantic segmentation과 같은 위치에 의존적인 작업에 zero-padding이 더 중요한 역할을 한 것을 볼 수 있습니다.
'컴퓨터비전' 카테고리의 다른 글
| [논문리뷰] Denoising Diffusion Probabilistic Models (DDPM) (3) | 2024.03.06 |
|---|---|
| [논문리뷰] VAE(Variational Auto-Encoder) (3) | 2024.02.28 |
| [논문리뷰] Masked Autoencoders(MAE) Are Scalable Vision Learners (0) | 2024.01.08 |
| [딥러닝] Faster R-CNN 논문 리뷰 (1) | 2022.03.24 |
| [딥러닝] Fast R-CNN 논문 리뷰 (0) | 2022.03.23 |




댓글