Abstract
최근 CNN의 발전에 힘입어 Monocular Depth Estimation(MDE) 분야에서 눈에 띄는 성과가 나타나고 있습니다. 이러한 CNN은 특징을 추출하는 인코더 부분과 이러한 특징을 바탕으로 깊이를 재구성하는 디코더 부분, 두 가지 주요 구성 요소로 나누어집니다. 인코더-디코더 구조는 strided convolution, pooling layers, skip connections, 그리고 multi-layer deconvolutional network 등과 같은 다양한 기술을 통합하여 깊이 추정의 효율성을 높이고 있습니다.
본 논문에서는 기존 기술을 뛰어넘어 더욱 정밀한 깊이 추정을 가능하게 하는 새로운 방법을 제안합니다. 특히, 인코더에서 추출한 특징들을 활용하여 디코더의 여러 단계에 걸쳐 local planar guidance layers를 구현함으로써, 더욱 세밀하고 정확한 깊이 맵을 재구성합니다.
Introduction
깊이 추정은 로봇 공학, 자율 주행 자동차 등 다양한 분야에서 핵심 기술로 자리 잡고 있습니다. 본 논문의 연구인 단안 이미지에서 깊이를 추정하는 분야의 연구 대부분은 CNN을 기반으로 하며, 일반적으로 인코더와 디코더라는 두 가지 주요 파트로 구성됩니다.
인코더는 VGG, ResNet, DenseNet과 같은 표준적인 백본 모델을 사용하여 특징을 추출합니다. 정밀한 깊이 추정을 위해 다양한 기술들이 적용되며, 일반적으로는 풀링(pooling)을 통해 해상도를 줄이고 수용 필드(receptive field)를 확장합니다. 최근에는 atrous spatial pyramid pooling(ASPP)이 도입되어 별도로 해상도를 낮추지 않고 컨볼루션 커널을 확장하여 특징을 추출하는 방식이 사용되었습니다. 이렇게 추출된 특징들은 디코더에서 단순한 업샘플링을 통해 깊이를 추정합니다.
본 논문에서는 디코더에서 단순한 업샘플링 방식을 넘어서, 여러 단계에 걸쳐 local planar guidance layers를 새롭게 도입하고 적용합니다. 각 단계에서 적용된 local planar guidance를 결합하여 최종 깊이를 추정합니다.
이러한 방식은 기존 multi-scale network나 pyramid 방식과는 2가지 측면에서 차이점이 있습니다:
- 기존 방식은 각 레이어의 출력을 해당 해상도에서 독립적으로 처리하여 전역 깊이를 추정하는 반면, 본 연구에서는 각 레이어에서 4차원 평면 계수(평면의 방정식을 활용함)를 학습하여 이 계수들로 깊이를 추정하고, 추정된 깊이를 독립적으로 처리하는 것이 아닌 한 번에 결합하여 사용합니다.
- 이러한 비선형 결과들의 결합으로, 각 해상도가 개별적으로 훈련이 된다고 주장하고 있습니다. 기존 방식은 낮은 해상도부터 점진적으로 결합하여 최종 깊이를 추정하여 손실 함수를 계산하고 점차적으로 gradient를 계산하는 방식이었다면, 이 방식은 각 해상도에서 추정된 깊이를 저장하여 최종 깊이 추정 때 한 번에 결합하는 방식으로 개별적으로 gradient가 계산된다는 것 같습니다.
이러한 접근법은 깊이 추정의 정밀도를 높이는 데 기여할 것으로 예상됩니다. 다음 파트에서 이에 대해 더 자세히 설명하겠습니다.
Method
네트워크 구조
네트워크 전체 구조는 아래와 같습니다.

기존 MDE와 같이 기본적인 인코더 디코더 구조를 가집니다. 인코더가 H / 8까지 해상도를 낮추어 특징을 추출하고, 다시 컬러 이미지의 해상도인 H까지 회복하여 깊이를 추정합니다.
- 1. Desne Feature Extractor(DFE): 앞선 전술한 백본 모델을 인코더로 적용하여, H / 8 해상도를 가지는 피쳐맵을 추출합니다.
- 2. ASPP: 확장 비율이 {3, 6, 12, 18, 24}를 활용하여 추출된 feature map에서 더 밀도가 높은 contextual 정보를 추출
- 3. Local planar guidance(LPG) layer: 디코더 파트의 각 단계에서 바람직한 깊이 추정을 위한 기하학적인 지침을 주기 위해 LPG를 적용하고, 각 단계에서 layer는 2배로 커진 해상도로 각 layer의 깊이를 추정
- 4. 최종 깊이 추정: 각 layer에서 추정된 깊이(\(c^{~k * k} \))들을 모두 결합하고, convolution layer를 거쳐 최종 깊이\( \tilde{d} \)를 추정
Local Planar Guidance(LPG) layer
이 LPG가 본 논문의 핵심 아이디어입니다. LPG를 적용함으로써 feature map과 최종 출력 사이의 직접적이고 명시적인 관계를 효과적으로 정의하였습니다.
기존 인코더로 추출한 feature map을 디코더 부분에서 단순 업샘플링하여 깊이를 추정하는 방식과 달리, 각 디코더 레이어에서 H / k의 해상도를 가지는 feature map가 k * k 패치에 맞는 4D 평면 계수를 추정하는 방식입니다. 여기 평면 계수를 추정하는 4개의 파라미터들만 활용하여 효과적으로 각 레이어에서 깊이를 추정할 수 있다고 제안합니다. 이러한 4D 평면 계수로 지역적인 평면에 가정을 주는 것은 기존 단순하게 업생플링하는 방식보다 효과적인 지침을 줄 수 있다고 합니다.
본 논문에서는 지역적인 평면에 가정을 주기 위해, 각 feature map에서 추정된 4D 평면 계수를 ray-plane intersection를 사용하여 k x k 패치의 지역 깊이 신호로 변환합니다. 아래 그림은 3D 공간에서 카메라가 있고, 이 카메라 평면에서 선택한 픽셀에서 나오는 광선이 평면에 교차하는 위치를 추출하는 과정입니다.

평면에서 \( {n_1}x + {n_2} y + {n_3} z + {n_4} = 0 \)는 고등학교 때 배운 평면의 방정식입니다. 본 논문은 현재 위치가 (0, 0, 0)이고 카메라 평면까지의 초점 거리는 1로 가정하였고, (\( x_i, y_i \))의 좌표에서 카메라 상에 맺히는 좌표는 (\( x_i, y_i, 1 \))이 됩니다. 여기서 우리가 구해야 할 평면까지 거리를 \( \tilde {c_i} \)라 가정하고, 카메라 상 좌표에 거리를 곱한 ( \( \tilde {c_i} x_i, \tilde {c_i} y_i, \tilde {c_i} \) )를 평면의 방정식에 대입해 주면 아래와 같은 식이 나옵니다.

이 (\( n_1, n_2, n_3, n_4 \))를 평면 계수이고, (\( u_i, v_i \)) 는 k x k 패치에서 정규화된 좌표값입니다. 아래 그림은 이 평면 계수를 추정하기 위한 LPG layer의 디테일입니다.

1 x 1 reduction에서 채널의 수가 3에 도달할 때까지 2배씩 줄여가며, 결정적으로 (H / k * H / k * 3)의 해상도를 얻습니다. 여기서 평면 계수를 추정하기 위해 2가지 방향 featuer map이 통과합니다:
- \( 1^{st}, 2^{nd} channels \): 극각(\( \theta \))과 방위각(\( \phi \))
- \( 3^{rd} channels \): 현재 위치와 평면간의 수직거리
먼저 극각(\( \theta \))과 방위각(\( \phi \))으로 아래와 같이 단위 백터인 \( n_1, n_2, n_3 \)를 구합니다(참고: https://ko.wikipedia.org/wiki/%EA%B5%AC%EB%A9%B4%EC%A2%8C%ED%91%9C%EA%B3%84).

그리고 현재 위치와 평면의 수직으로 떨어진 거리 Sigmoid 함수로 0~1 사이 값으로 변환해, 현재 데이터셋 도메인의 최대거리(\(k\)를 곱하여 수직 거리 \( n_4 \)를 구하고, 위에서 정의한 Equation 1로 각 픽셀의 깊이를 추정하고, 결합하여 각 k x k 패치의 깊이를 추정(\( c^{~k * k } \))합니다.
서로 다른 단계의 특징들이 결합되어 최종 깊이 추정을 하기 때문에 global 및 local의 정보들을 모두 결합할 수 있고, 서로서로의 단점은 보완해 줄 수 있다고 제시합니다. 최종 결합되어 깊이추정을 하는 도식은 아래와 같습니다.
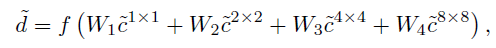
\( f \)는 활성화 함수이며 \( W_1, W_2, W_3, W_4 \)는 Convolution으로 선형 변환을 하는 것입니다. 중간 단계에서 산출된어떠한 깊이에도 손실함수다 반영되지 않으며, 오로지 최종적으로 형성된 깊이(\( \tilde {d} \))에서만 훈련이 진행되기 때문에 뾰족한 boundary 같은 세부 사항은 더 작은 스케일에서, 큰 구조는 더 큰 스케일에서 학습될 것이라고 굳게 믿고 있습니다.

노란색 경계선부터 까만색까지 1/8 ~ 1/1의 해상도이며, 빨간색 경계선은 모든 스테이지의 결과를 결합한 것입니다. 파란색과 까만색 경계선에서 자동차 테두리와 같은 미세한 세부사항이 인식이 잘 되었는 반면, 노란색과 초록색 경계선에는 이 부분을 인식하지 못했습니다. 이렇게 윗 단계에서 잃어버린 정보를 더 낮은 단계에서 복원하며 더 정밀한 깊이 추정이 가능합니다.
Experiments
이 파트에서는 시각적인 부분은 생략하고, 간단한 정량적인 부분만 비교하겠습니다. 자세한 내용은 본 논문을 참고해주시길 바랍니다.
NYU Depth V2 데이터 셋을 사용하였을 때 기존 모델(인코더와 심플한 업샘플링의 디코더)보다 더 나은 성능을 기록한 것을 볼 수 있습니다.
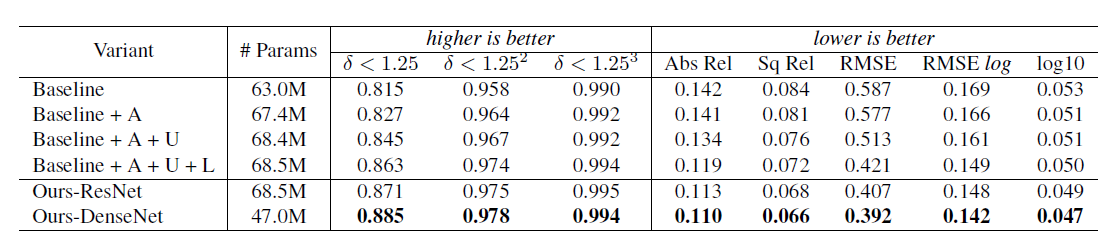
확실히 Local planar guidance layers를 적용하였을 때, 성능이 확 좋아진것을 볼 수 있습니다.
오늘은 새로운 디코더 Layer 접근 방식인 BTS 논문을 한 번 리뷰 해보았습니다.
BTS라는 이름만 보고 설마 했지만, 역시 저희의 우리나라의 논문인 것을 확인할 수 있었습니다.
자세한 내용은 본 논문을 참고하시고, 언제나 게시글에 대한 피드백은 환영입니다.
긴 글 읽어주셔서 감사합니다.


댓글