[논문리뷰] CPVT(CONDITIONAL POSITIONAL ENCODINGS FOR VISION TRANSFORMERS)
참조
[논문리뷰] AN IMAGE IS WORTH 16X16 WORDS:TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE(Vision Transformer)
참고 자료 [논문리뷰] Attention is All you need의 이해 소개 Attention Is All You Need The dominant sequence transduction models are based on complex recurrent or convolutional neural networks in an encoder-decoder configuration. The best perfor
lcyking.tistory.com
들어가며
본 글은 Vision Trasnformer(ViT)에 대한 사전지식이 있다는 가정하에 작성되었습니다.
기존 컴퓨터 비전에는 CNN이 거의 지배적인 구조로 사용되었지만, Transformer 구조가 나타나고 이 구조를 비전에 활용한 ViT가 게재되며 많은 각광을 받고 있었습니다. 이 구조는 각 픽셀을 패치로 나누고, 이 패치들을 토큰들로 사용하는 것으로 시작합니다.
위와 같은 토큰들은 위치가 바뀌어도 같은 값을 출력하는 Permutation-invariant의 제한점이 있어, Absolute Position Encoding을 해주어 각 토큰의 위치 정보를 입력해주는 방식으로 이러한 제한점을 극복해왔지만 여전히 아래와 같이 몇 가지 제한점이 존재한다고 합니다.
- Training에 사용되는 Position Encoding은 입력 이미지 크기에 대비한 고정된 크기라서, Inference 시 이미지 크기가 바뀐다면 적용 불가
-> 이것을 개선하기 위해, 바뀐 크기에 따라 Position Encoding을 Interpolation 하는 방법을 적용하였지만 Fine-Tuning 없이는 성능이 좋지 않았음 - 일반적으로 비전 Task는 객체의 위치가 변해도 같은 객체를 인식하는 Translation Equivalence를 원하는데, 기존 Position Encoding은 객체에 상관없이 픽셀의 위치에 따라 고유한 값을 입력하는 방식인 Absolute Position Encoding를 입력하기 때문에 성립하기가 힘듦
-> 이를 개선하기 위해, 각 픽셀의 지역적인 관계를 잘 고려하는 Relative Position Encoding을 삽입하였지만 이론상으론 맞으나 성능은 Absolute 값을 입력하는 방식보다 저조
이러한 제한점들로 본 논문은 Position Encoding의 새로운 접근 방법인 Conditional Position Encoding(CPE)를 제안하였습니다. CPE는 Training과 Inference에 해상도 크기가 달라도 동적으로 Position Encoding이 가능하고, 입력 토큰들의 지역적인 관계를 잘 고려하는 Relative Position Encoding의 이론을 그대로 가져갔습니다.
결과적으로, 본 논문은 Relative Position Encoding의 이론은 가져가며, Fine-Tuning 없이도 동적으로 해상도에 맞춰 잘 적응되어 좋은 성능을 내는 것이 실험으로 입증되었습니다.
Conditional Positional Encoding(CPE)
사실 서론에서 거창하게 많이 이야기했지만 작동 방식과 코드는 생각보다 간단합니다. 일단 성공적인 Position Encoding을 위해서는 3가지 요구사항이 필요하다고 합니다.
- 토큰들의 위치가 바뀌면 결과도 바뀌는 Permutation-variant와 객체의 위치 변화에 덜 민감한 Translation-equivariance
- Training과 Inference에서 이미지 해상도 변경에 따른 동적 변화
- 어느정도 Absolute position의 능력을 가져야 함
3번의 요구 사항을 보면 Absolute Position의 능력을 가진다는 게 좀 의아할 수도 있습니다. 위에서는 Absolute Position을 넣는다는게 제한사항에 있어, 지역적인 관계를 잘 고려해야 한다고 했는데 말이죠. 본 논문에서는 아래와 같은 결과로 이 주장을 펼쳤습니다.

첫 번째가 Position Encoding을 적용하지 않은 것, 두번째와 세 번째는 Absolute Position을 적용한 것, 네 번째는 Relative Position을 적용한 결과입니다. Absolute Position을 적용한 것이 나머지 Position보다 성능이 더 우월한 것을 볼 수 있습니다. 본 논문은 이러한 근거에 따라 이 Absolute Position도 어느정도 필요하다고 주장하고 있습니다.
CPE는 위 3가지 요구사항을 Positional Encoding Generator(PEG)를 제안하며 해결하였습니다.
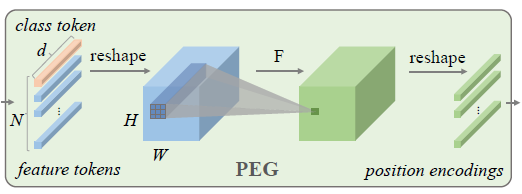
PEG는 기존 feature tokens을 단순하게 Convolution 연산하는 것입니다. 먼저, input sequence \( X \in \mathbb {R}^{B * N * C} \)에서 class token과 feature tokens을 분해하고, feature tokens만 feature map 형태인 \( X^{'} \in \mathbb {R}^{B * H * W * C} \) 형태로 reshape 합니다. 그 후, \( X^{'} \)에서 PEG로 위치 정보를 넣어줍니다. PEG는 zero padding을 포함한 3 * 3 convolution layer 입니다. 최종적으로 다시 (B, N, C) 형태로 reshape 하여 feature tokens에 대한 position encodings을 생성합니다.
이 단순한 과정이 3가지 요구사항을 아래와 같이 충족한다고 주장하고 있습니다.
- Permutation-variant, Translation-equivariance
- 아래 그림과 같이 Input Sequence의 순서를 무작위로 섞었을 때, 3 * 3 Convoution에 각각 다른 값이 대응되어 다른 Position Encoding 값이 도출되기 때문에 Permutation-variant

- 또한 위 그림에서 3 * 3 Convolution의 순서는 변하지 않기 때문에, 기존 CNN의 Trasnlation-equivariant 성질을 가짐
- 아래 그림과 같이 Input Sequence의 순서를 무작위로 섞었을 때, 3 * 3 Convoution에 각각 다른 값이 대응되어 다른 Position Encoding 값이 도출되기 때문에 Permutation-variant
- 해상도에 크기에 비례하여, Convolution의 크기와 Weight는 변하지 않고, 커널이 순회하는 숫자만 조절되기 때문에, 동적 변화를 성립
-> 만약 3 * 3 Conv에 6 * 6 해상도와 8 * 8 해상도가 있다면 각각 4 * 4번 순회, 6 * 6번 순회로 동적 변화 - 토큰 가장자리에 0의 패딩을 넣으면서, Absolute Position 성립(0 패딩에 따른 Absolute Position 참고 자료).
위와 같은 증거로 간단한 Convolution으로 가능하게 할 수 있었습니다.
그리고, 본 논문은 Class_Token을 없애고, 단순하게 Glocal Average Pooling(GAP)으로 이미지 분류를 하는 심플한 방법 또한 제시하였습니다.

이렇게 단순한 연산으로 위치 정보를 성공적으로 삽입할 수 있었다고 합니다.
마치며
사실 제안하는 기술을 별 거 없긴한데, 이론적으로 그럴싸한 부분이 많았습니다. 저만 그렇게 생각하는지 모르겠지만 솔직히 그냥 실험하다 보니 잘 된 거 아니냐 라는 의심을 품었는데, 기존에 Q, K, V 전체에 삽입했던 PEG를 Q, K에서만 삽입해도 결과가 잘 나왔다고 합니다.
그리고, 아래는 기존 CPVT와 CPVT-GAP에 대한 비교 실험입니다.
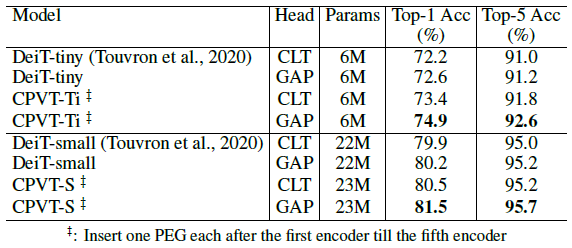
수용 필드에 대한 실험도 진행하였습니다.
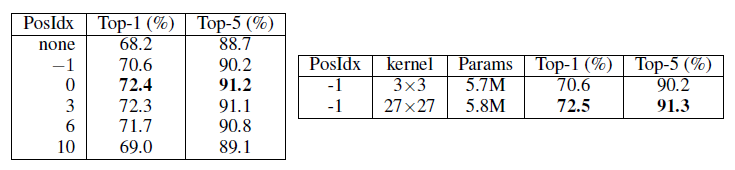
왼쪽 그림의 PosIdx가 Positional Encoding을 삽입한 레이어의 위치인데, -1이 Transformer Encoder에 삽입되기 전입니다(0은 첫 번째 Encoder에 삽입된 후). 당연히 0번째가 Attention연산을 한번 했기 때문에 수용필드가 더 큽니다. 따라서, 수용필드가 크면 Position encoding이 잘 되는구나 하는 가설을 세우고, PosIdx = -1에서 PEG의 커널 사이즈를 27 * 27로 늘리고 돌린 결과가 오른쪽입니다. 가설이 증명되었네요.
마지막으로 Absolute Position을 삽입해주었던 zero padding의 효과가 실제로 있는지에 대한 실험도 진행하였습니다.

세 번째의 1( 12 x)이 1*1 Convolution을 적용했다는 건데, 패딩이 적용되지 않으니 성능이 급격하게 떨어진 것을 볼 수 있습니다.
오늘은 CPVT의 논문을 리뷰해 보았습니다.
긴 글 읽어주셔서 감사합니다.