[논문리뷰] Swin Transformer v2: Scaling Up Capacity and Resolution

참조

 

[논문리뷰] Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

 

들어가며

 

본 글은 제목 그대로 Swin Transformer의 후속작입니다. 그렇기 때문에 Swin Transfomrer의 사전 지식이 있다는 가정 하에 작성되었습니다.

 

기존 Transformer는 NLP 도메인에서는 모델이 커지거나 시퀀스가 길어지면 지속해서 성능이 올라가는데, Swin에 사용된 Transformer는 모델의 용량이 커지고, 해상도가 올라감에 따라 성능 향상에 한계가 있다고 지적합니다. 이러한 제한사항에 3가지 문제점을 제기하였습니다.

 

• 학습의 불안정성
  

  

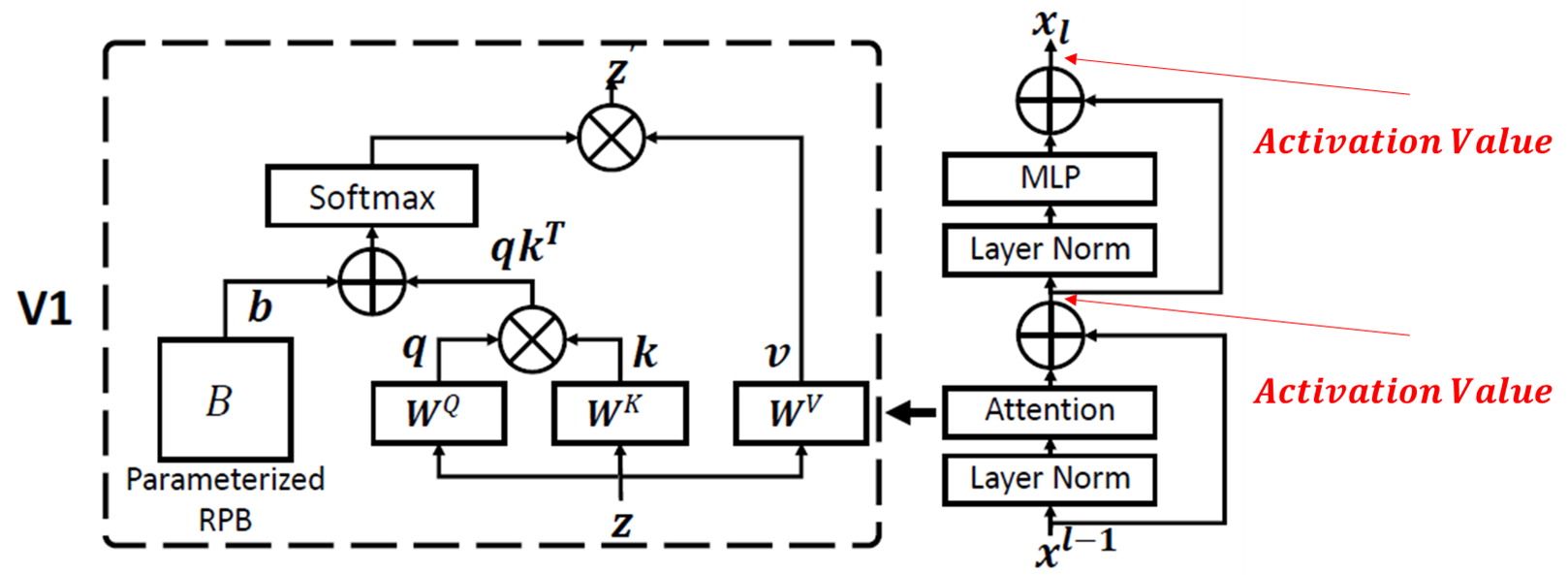
  그림 1

  
  -> 위 Attention 연산, MLP 연산 후 Residual Conntection으로 연결된 부분이 Activation Value인데, 이 값이 Layer-by-Layer로 축적되어 Layer가 깊어질수록 이 불일치가 커집니다. 아울러, 모델이 커질수록(즉, 파라미터수가 더 많은 모델) 이 불일치가 더 심해지며, 학습에 불안정성을 초래.
  
  
• Pre-training과 Fine-tuning의 해상도 차이
  
  -> 백본에 ImageNet과 같은 저해상도로 사전 학습되고, Object Detection, Semantic Segmentation, 더 큰 해상도를 가지는 ImageNet 등, 고해상도의 Fine-tuning을 할 때, 기존 Swin의 Position Encoding은 저해상도에서 고해상도로 단순한 Interpolation이 이루어짐.
  
  
• Labeled data 부족
  
  -> 기존 Swin은 Labeled data에 대한 의존도가 강하며, 이에 따라 성능이 크게 좌우함.

 

 

이러한 제한점을 해결하기 위해, 여러 가지 제안 사항을 내놓았습니다. 그 결과로 모델의 용량이 커지고, 해상도가 올라감에 따라 성능의 지속적인 향상을 확인하였습니다. 자세한 내용은 아래에서 살펴보겠습니다.

 

Swin Tranformer V2

 

Swin V2는 기존 Swin과 거의 같은 구조인데, 약간의 미세한 부분에 대한 수정만이 이루어졌습니다.

 

앞선 제한점은 학습의 불안정성, 사전 학습과 미세조정의 해상도 차이, Labeled data 부족으로 총 3가지였습니다.

 

 

학습의 불안정성

어떻게 학습이 불안정한지 그림으로 먼저 보겠습니다.

그림 2

 

위 그림에서 Pre로 표기된 것의 그래프를 보면, 레이어가 깊어질수록 값이 점진적으로 커지는 것을 볼 수 있고, 이는 해상도가 더 커질수록 심해집니다. 

 

이에 따라 아래와 같이 Loss도 발산합니다. 

 

그림 3

 

본 논문은 이런 제한사항을 아주 간단한 구조 조정으로 해결하였습니다. 다시 그림 1에서 Attention Value가 추출되는 과정을 보면, Attention이나 MLP 전에 LayerNorm(LN)이 위치해 있는 Pre-Norm이였는데, 이것은 아래와 같이 Post-Norm으로 바꿨습니다. 

 

 

위 간단한 구조 조정으로 인해, Attention 및 MLP 연산 후 LN이 이루어지기 때문에 Activation Value가 점진적으로 커지는 것을 막을 수 있답니다. 

 

또한, 기존 Attention은 Dot-Product 연산으로, 전체 네트워크에서 몇몇의 헤드와 블록의 Pixel pair에만 값이 지배적이라고 합니다. 그렇기 때문에, 아래와 같이 새롭게 Attention 연산을 정의하였습니다. 

 

\( B_{ij} \): Positional Encoding

 

각 헤드별로 파라미터를 공유하지 않는 독립적 \( \tau \)를 정의하여 몇몇의 헤드나 블럭에 치우치지 못하도록 하였습니다. 아울러, 기존 Dot-Product를 Cosine 유사도로 변경하며 위 Activation Value의 정규화에 도움을 주었다고 합니다. 

 

 

사전학습과 미세조정의 해상도차이

기존 Swin은 저해상도에서 학습된 Relative Position Encoding이 고해상도로 전이될 때 단순한 Interpolation이 이루어진다고 하였습니다(Relative Position Encoding에 대한 것이 어떻게 이루어지는지는 참조의 Swin Transformer에 자세히 기술하였으니 참고하시길 바랍니다).

 

이 저해상도에서 고해상도로 전이 과정을 좀 더 부드럽게 하기 위해, 본 논문은 log-spaced continuous position encoding을 제안하였습니다.

 

이 방법은 아주 가벼운 MLP를 활용한 방법입니다. 

 

 

위 수식에서 \( \mathcal {G} \)가 MLP이고, \( \Delta x, \Delta y \)는 Relative Coordinates입니다. MLP는 2-layer와 RELU로 구성되었고, 입력은 2(좌표)이고 출력은 헤드의 수입니다. 이렇게 함으로써 각 헤드에 대해 서로 다른 Relative Position Encoding이 되고, 해상도가 증가하더라도 Relative Coordinates를 이 MLP에 입력해주기만 하면 부드럽게 확장이 가능하다고 주장합니다. 

 

그리고, 저해상도에서 해상도로 전이할 때 Relative Coordinates도 상대적으로 커지므로 이 좌표에 log를 씌웠다고 합니다.예컨대, 8 * 8 window size에서 16 * 16 window size로 전이한다고 했을 때 기존 방법은 [-7, 7] * [-7, 7]이 [-15, 15] * [-15, 15]로 전이되어 \( \frac {8} {7} = 1.14 \)의 확장이 이루어져야 하는데, log를 씌우면 [-2.079, 2.079] * [- 2.079 , 2.079 ]이 [-2.773, 2.773] * [-2.773, 2.773]로 확장이 이루어져 0.33 만큼의 확장만 이루어집니다. 

 

 

Labeled data 부족

마지막으로 Labeled data가 부족한 것은 Self-supervised learning 방법인 SimMIM을 활용하여 해결하였습니다(SimMIM은 추후에 다루도록 하겠습니다). 이렇게 하여 기존 labeled data의 1/40 분량만을 사용하여 SOTA 성능을 내었다고 합니다.

 

 

마치며

 

 

위와 같은 개선 사항들로 기존 Swin보다 높은 성능을 기록하였습니다. 

 

 

 

오늘은 Swin V2 논문을 리뷰해 보았습니다.

긴 글 읽어주셔서 감사합니다.