[논문리뷰] Monocular Depth Estimation Using Laplacian Pyramid-Based Depth Residuals(LapDepth)
Abstract
딥러닝의 많은 발전으로 Monocular Depth Estimation(MDE)에도 여러 Encoder-Decoder 구조가 접목되고 있습니다. 그러나 대부분 Decoding 절차에서 반복되는 심플한 업샘플링 연산은 잘 인코딩 된 features의 특성을 완전히 활용하지 못하는 제한점이 있습니다. 본 논문은 이러한 제한점을 해결하기 위해 본 논문에서는 Laplacian pyramid를 도입하였습니다. 이 방법은 인코딩 된 Features가 Laplacian pyramid의 분해에 의해 깊이 잔차들로 디코딩되고, 디코딩된 출력들이 점진적으로 결합하여 최종 깊이 맵을 형성 합니다.
위와 같은 방식으로 깊이 맵을 형성함으로써 global 한 깊이부터 boundary 같은 local 한 깊이까지 잘 추정이 된 것을 확인할 수 있었습니다. 또한, Convolution blocks에 사전 Weight Standardization을 적용하여 gradient의 흐름의 향상을 돕고, 최적화를 더 쉽게 도왔습니다.
네트워크의 실험적인 결과는 실내, 실외 데이터 세트에서 기존 State-of-the-Art 모델과 비교했을 때 우수한 성능을 거두었음을 확인할 수 있습니다. 아래 섹션에서 차차 살펴보겠습니다.
Introduction
심층 신경망(DNN)을 이용한 모델의 큰 성공으로 인해, 많은 연구자들이 Monocular Depth Estimation을 컬러 이미지에서 깊이 이미지로 변환하는 문제로 공식화하기 시작했습니다. 깊이 정보와 관련된 Features를 추출하기 위해 CNN이 주로 채택하여 컬러와 깊이 값 사이의 관계를 잘 인코딩할 수 있었습니다. 하지만 이러한 접근 방식은 깊이 Boundary에서 여러 가지 모호성이 발생하고 있었습니다.
기존방식은 잘 알려진 VGG, ResNet과 같은 인코더들을 통과하여 얻은 Latent Features를 단순하게 업샘플링하여 깊이를 추정하기 때문에 다양한 스케일 레벨에서 객체들의 Boundary가 희미해지면서 부정확한 깊이 값들을 산출할 가능성이 있다고 합니다.
본 논문에서는 기존 방식의 단점을 극복하기 위해, Laplacian pyramid 기반 디코더 아키텍처를 활용하여 인코딩 된 features롸 최종 출력 깊이 맵 간의 관계를 정밀하게 해석하는 기술을 제안하였습니다. 각 Pyramid 레벨에서 컬러 이미지의 Laplacian 잔차를 구하고 인코딩 된 features와 함께 디코딩되어 깊이 잔차를 생성하고, 이러한 깊이 잔차들을 각 피라미드 레벨에서 점진적으로 결합하여 더 나은 깊이의 Boundaries를 예측할 수 있다고 합니다.
기존 반복되는 업샘플링 연산 대신 Laplacian pyramid의 서로 다른 레벨들에서 계산된 이러한 Boundary의 정보를 결합함으로써, 인코딩 된 features를 더 효과적으로 활용하여 정확한 깊이 추정이 가능하게 됐습니다. 또한, Convolution blocks의 사전 Weight Standardization를 적용하여, 수렴을 더욱 안정화되게 하였습니다.
간략하게 전반적인 흐름을 살펴봤고, 아래는 세부적인 내용입니다.
Proposed Method
본 논문은 Laplacian pyramid 기술을 디코딩 절차에 활용하여, global, local 두 가지 정보를 통합하였습니다. 제안하는 기여는 크게 두가지로 나뉩니다.
- 디코딩 절차에서 컬러 이미지로 부터의 Laplacian 잔차를 구하여 적절하게 표현되는 local 정보를 이용하여, 더 뚜렷한 Boundary를 추정
- Convolution block 앞에 Weight Standardization을 적용하여 대부분 0으로 수렴되는 깊이 잔차들의 안정화
전반적인 구조는 아래와 같습니다.

이렇게 보면 아주 복잡해 보이지만, 천천히 살펴보겠습니다.
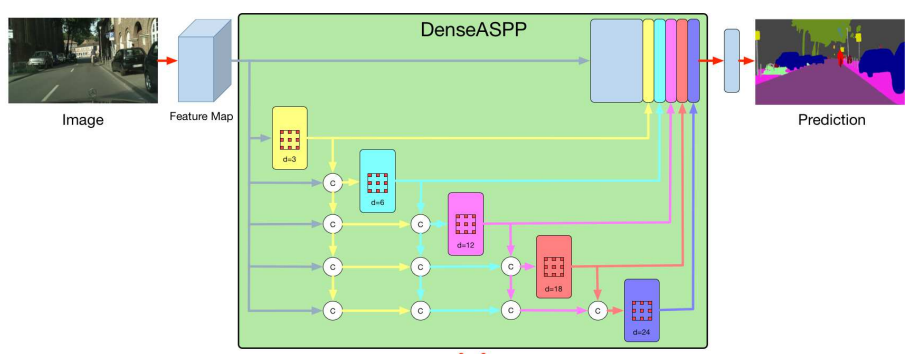
- pre-trained encoder: VGG, ResNet, DenseNet, ResNext과 같은 범용적으로 사용하는 Backbone 모델입니다. 위 그림에서는 ResNext101을 사용하였습니다(뒤에 숫자는 층의 개수를 의미합니다). 첫 레벨인 layer3에서 S/16의 해상도를 가지는 출력에서는 다양한 장면 정보를 얻기 위해, dilation 비율이 각 3, 6, 12, 18인 DenseASPP 기술을 접목시켰고 나머지 구조에서는 Laplacian pyramid 구조를 따릅니다.
- Laplacian pyramid: 여러 분기의 레벨들(\( R_5 \) ~ \( R_1 \)).
- \( R_5 \): 가장 높은 레벨로 DenseASPP를 거쳐 Global 장면 정보를 추출
- (\( R_4 \) ~ \( R_1 \)) : 나머지 레벨들은 입력 컬러 이미지의 Laplacian 잔차 (\( L_4 \) ~ \( L_1 \))를 활용하여 각 레벨에서 출력된 latent features(\( x_1 \) ~ \( x_4 \))를 가이드하여 깊이 잔차를 생성합니다.
- 최종 깊이 (\( D^~_5 \) ~ \( D^~_1 \)): 출력된 깊이 잔차들(\( R_4 \) ~ \( R_1 \))이 행렬합으로 각각 의 깊이 맵을 출력 합니다.
- 위 모든 과정의 Convolution의 커널은 3 x 3입니다
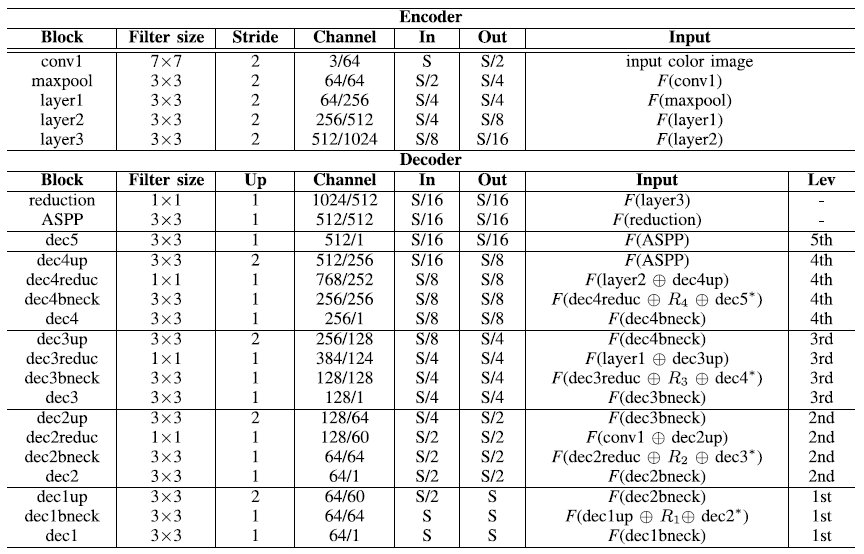
깊이 잔차
먼저, 컬러 이미지에서 Laplacian 잔차를 구하는 방법은 아래와 같습니다.

k는 Laplacian pyramid에서 각 레벨의 index를 의미하고, \( I_k \)는 k 레벨의 컬러 이미지를 의미합니다(각 레벨의 해상도는 \( 1 / 2^{k-1} \)의 스케일). Up()은 기본적인 bilinear interpolation입니다.
현재 k 레벨의 깊이 잔차(\(R_k\))는 위에서 추출한 현재 레벨의 Laplacian 잔차(\(L_k\)), latent features(\(x_k\)), 위 레벨(k+1)에서 구한 깊이 잔차를 결합하고, 이 결합된 features에 Convolution 블록들을 쌓고 Laplacian 잔차(\(L_k\))를 한 번 더 행렬합을 해주어 구합니다.

\( B_k \)로 출력된 결과는 1차원 깊이 맵이고, 잔여 학습이 이루어지는 \( L_k \) 또한 동일한 차원입니다(본 논문의 github에서 제시한 코드를 분석해 봤을 때 여러 채널로 구성된 \(L_k\)를 채널기준으로 평균을 내어 1차원 깊이맵으로 변환하였고, 수렴에 안정화를 위해 0.1만큼 가중치를 두었습니다). 이 디코딩 과정에서 \( L_k \)는 동일한 스케일 공간의 local 정보를 정확하게 복원하도록 가이드하는 역할을 하고, 깊이 boundary를 정확하게 나타내는데 도움을 준다고 제시하고 있습니다.
위에서 산출한 깊이 잔차(\( R_k \))를 통해 최종 깊이맵은 아래와 같이 점진적으로 연산됩니다.

Weight Standardization
본 논문에서는 디코딩 과정을 더 효과적으로 하기 위해 Convolution block앞에 Weight Standadization이라는 활성화 함수를 적용합니다. 깊이 잔차들의 반복적인 합으로 깊이 맵을 연산하는 과정에서 음과 양의 값을 균형 있게 포함하는 것이 안정적이고 정확한 깊이 정보를 추정하기 위해 바람직하다고 제시합니다.

- (a) 같은 경우는 최종적으로 ReLU를 이용하기 때문에 기존 음의 값들이 0으로 상쇄됩니다.
- (b) 같은 경우는 이를 완화하기 위해 사전 활성화 함수를 뒀지만, 깊이 잔차의 대부분은 0을 가지므로 학습 중에 gradient vanishing 문제로 이어질 수 있다고 합니다.
- (c)는 Weight Standardization을 사전에 두어 기울기가 0으로 소실하는 문제를 극복했습니다.
손실 함수
손실 함수는 크게 data loss \( L_d \)와 gradient loss \( L_g \) 두 가지로 구성됩니다.

여기서 \( \alpha \)와 \( \beta \)는 각 요소의 밸런스를 조절하기 위한 하이퍼 파라미터이며 10과 0.1로 설정되었습니다. data loss는 일반적으로 MDE에서 사용하는 손실 함수이고, Gradient loss는 본 논문에서 local 정보인 깊이의 boundary를 잘 추정하기 위해 도입하였습니다.
- Data Loss
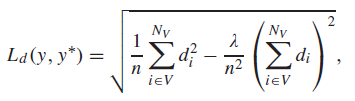
기존과 동일하고 \( d_i = logy_i - logy^*_i \)입니다. \( \lambda \)는 기존 논문들과 동일하게 0.85로 설정되었습니다.
- Gradient loss

새로 도입된 loss 함수입니다. 깊이 boundaries에 local details를 강화하기 위해, 깊이 맵의 그래디언트를 활용합니다. 고정된 weight를 가진 Convolution을 적용합니다. gt의 희박한 깊이 데이터는 수평, 수직에서 그래디언트를 정확하게 계산하는 데 어려움을 주기 때문에, 수평, 수직 두 가지에서 고정된 Weight를 사용하여 계산합니다(코드에서는 수평: [[1, 0, -1], [2, 0, -2], [1, 0, -1]], 수직: 수평의 Transpose). 위의 m는 채널의 평균을 의미하는 함수이고, 각 y의 아래 첨자 h, v는 각각 수평과 수직입니다. N은 총픽셀의 개수이고 i는 각 픽셀의 인덱스입니다. 이 함수를 적용하고 확연한 차이를 보였습니다.

Experimental results
시각적인 실험 결과는 논문을 참고하시길 바랍니다.
아래는 Laplacian pyramid의 레벨의 수를 나타내는 비교 실험입니다. 레벨이 올라갈수록 성능이 증가하는 것을 볼 수 있으며 아마 7 레벨이 한계일 것 같습니다.

아래는 Weight Standardization을 적용하였을 때 결과입니다. 확연하게 성능이 많이 올라간 것을 볼 수 있습니다.

마지막으로 아래는 여러 가지 pyramid 방법을 적용하였을 때의 결과입니다. Laplacian을 사용하였을 때 가장 높은 성능을 기록하였습니다.

오늘은 새로운 피라미드 방법인 Laplacian Pyramid를 MDE에 적용한 결과를 살펴보았습니다.
자세한 내용은 본 논문을 참고하시고, 언제나 게시글에 대한 피드백은 환영입니다.
긴 글 읽어주셔서 감사합니다.